题目内容
 如图,A为直线y=x上一点,AB⊥x轴于B点,双曲线y=
如图,A为直线y=x上一点,AB⊥x轴于B点,双曲线y=| k |
| x |
考点:反比例函数系数k的几何意义
专题:计算题
分析:通过解方程组
得D(
,
),再表示出A(4,4),C(4,
),根据反比例函数k的几何意义得到S△OCB=
k,则S△ODC=
k,然后利用S△OBC+S△ODC+S△ADC=S△AOB得到
k+
k+
•(4-
)•(4-
)=
•4•4,整理得k+6
-8=0,然后解关于
的一元二次方程即可得到k的值.
|
| k |
| k |
| k |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
| k |
| 4 |
| k |
| 1 |
| 2 |
| k |
| k |
解答:解:解方程组
得
或
,则D(
,
),
∵B(4,0),AB⊥x轴,
∴A(4,4),C(4,
),
∵S△OCB=
k,
而S△ODC:S△OBC=3:2,
∴S△ODC=
k,
∵S△OBC+S△ODC+S△ADC=S△AOB,
∴
k+
k+
•(4-
)•(4-
)=
•4•4,
整理得k+6
-8=0,解得k=4.
故答案为4.
|
|
|
| k |
| k |
∵B(4,0),AB⊥x轴,
∴A(4,4),C(4,
| k |
| 4 |
∵S△OCB=
| 1 |
| 2 |
而S△ODC:S△OBC=3:2,
∴S△ODC=
| 3 |
| 4 |
∵S△OBC+S△ODC+S△ADC=S△AOB,
∴
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
| k |
| 4 |
| k |
| 1 |
| 2 |
整理得k+6
| k |
故答案为4.
点评:本题考查了反比例函数系数k的几何意义:在反比例函数y=
图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.也考查了反比例函数与一次函数的交点问题.
| k |
| x |

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
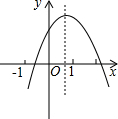 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0 ②2a+b<0 ③4a-2b+c<0 ④
| 4ac-b2 |
| 4a |
其中正确结论的个数为( )
| A、4个 | B、3个 | C、2个 | D、1个 |
 如图所示,把一张长方形的纸片沿着AB折叠,若∠1=50°.则∠2的度数为( )
如图所示,把一张长方形的纸片沿着AB折叠,若∠1=50°.则∠2的度数为( )| A、40° | B、50° |
| C、65° | D、75° |
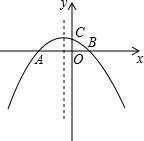 如图,抛物线y=-
如图,抛物线y=- 如图,等边△ABC外一点P到三边距离分别为h1,h2,h3,且h3+h2-h1=3,其中PD=h3,PE=h2,PF=h1.则△ABC的面积S△ABC=
如图,等边△ABC外一点P到三边距离分别为h1,h2,h3,且h3+h2-h1=3,其中PD=h3,PE=h2,PF=h1.则△ABC的面积S△ABC= 如图,△ABC的位置如图,
如图,△ABC的位置如图,