Question

如图，已知两条线段AB∥CD，点E不在AB、CD所在的直线上．∠ABE=α，∠CDE=β，∠BED=γ．当E点在不同位置时，α、β、γ之间的数量关系也会有所不同．请你再画出两种不同的情况，并写出α、β、γ之间的数量关系．

Answer 1

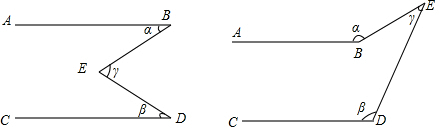
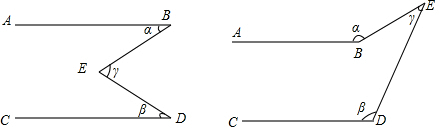
考点：平行线的性质

专题：

分析：在图1中过点E作EF∥AB，根据平行线的性质可得出结论；在图2中延长AB交DE于点F，先根据平行线的性质得出∠β=∠BFE，再由三角形外角的性质可得出结论．

解答：解：在图1中过点E作EF∥AB，
∵AB∥CD，
∴AB∥CD∥EF，
∴∠α=∠BEF，∠β=∠DEF，
∴∠α+∠β=∠γ；
在图2中延长AB交DE于点F，
∵AB∥CD，
∴∠β=∠BFE．
∵∠α是△BEF的外角，
∴∠α=∠γ+∠BFE，即∠α=∠γ+∠β．
如图3，可得∠α+∠β+∠γ=360°；
如图4，可得∠α+∠β+∠γ=180°．

点评：本题考查的是平行线的性质，根据题意作出辅助线，构造出平行线是解答此题的关键．