题目内容
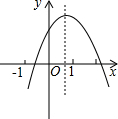 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0 ②2a+b<0 ③4a-2b+c<0 ④
| 4ac-b2 |
| 4a |
其中正确结论的个数为( )
| A、4个 | B、3个 | C、2个 | D、1个 |
考点:二次函数图象与系数的关系
专题:
分析:由抛物线开口方向得a<0,由抛物线对称轴在y轴的右侧得a、b异号,即b>0,由抛物线与y轴的交点在x轴上方得c>0,所以abc<0;根据抛物线对称轴的位置得到-
<1,又a<0,则根据不等式性质即可得到2a+b<0;由于x=-2时,对应的函数值小于0,则4a-2b+c<0;根据抛物线与x轴有2个交点得到b2-4ac>0,即4ac-b2<0,又a<0,则根据有理数除法法则得到
>0.
| b |
| 2a |
| 4ac-b2 |
| 4a |
解答:解:∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴在y轴的右侧,
∴x=-
>0,
∴b>0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,故①错误;
∵-
<1,a<0,
∴2a+b<0,故②正确;
∵当x=-2时,y<0,
∴4a-2b+c<0,故③正确;
∵抛物线与x轴有2个交点,
∴b2-4ac>0,即4ac-b2<0,
又∵a<0,
∴
>0,故④正确.
综上所述,正确结论有3个;
故选:B.
∴a<0,
∵抛物线的对称轴在y轴的右侧,
∴x=-
| b |
| 2a |
∴b>0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,故①错误;
∵-
| b |
| 2a |
∴2a+b<0,故②正确;
∵当x=-2时,y<0,
∴4a-2b+c<0,故③正确;
∵抛物线与x轴有2个交点,
∴b2-4ac>0,即4ac-b2<0,
又∵a<0,
∴
| 4ac-b2 |
| 4a |
综上所述,正确结论有3个;
故选:B.
点评:本题考查了二次函数的图象与系数的关系:二次函数y=ax2+bx+c(a≠0)的图象为抛物线,当a>0,抛物线开口向上;对称轴为直线x=-
;抛物线与y轴的交点坐标为(0,c);当b2-4ac>0,抛物线与x轴有两个交点;当b2-4ac=0,抛物线与x轴有一个交点;当b2-4ac<0,抛物线与x轴没有交点.
| b |
| 2a |

练习册系列答案
相关题目
 如图所示,a∥b,∠1=158°,∠2=42°,∠4=50°.那么∠3=( )
如图所示,a∥b,∠1=158°,∠2=42°,∠4=50°.那么∠3=( )| A、50° | B、60° |
| C、70° | D、80° |


 如图,A为直线y=x上一点,AB⊥x轴于B点,双曲线y=
如图,A为直线y=x上一点,AB⊥x轴于B点,双曲线y= 如图,将矩形纸片ABCD按如图方式折叠,使点D与点B重合,折痕为EF,若S△ABE:S△BFE=4:5,则tan∠BFE=
如图,将矩形纸片ABCD按如图方式折叠,使点D与点B重合,折痕为EF,若S△ABE:S△BFE=4:5,则tan∠BFE= 一副三角板按如图所示放置,其中∠F=∠ACB=90°,∠E=30°,∠A=45°,点C在FD的延长线上,点B在DE上.
一副三角板按如图所示放置,其中∠F=∠ACB=90°,∠E=30°,∠A=45°,点C在FD的延长线上,点B在DE上.