题目内容
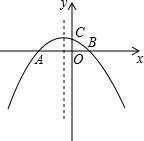 如图,抛物线y=-
如图,抛物线y=-| 1 |
| 9 |
| 1 |
| 3 |
考点:抛物线与x轴的交点
专题:
分析:根据抛物线的解析式求得B、C的坐标以及对称轴方程,然后连接BC并延长,交抛物线的对称轴x=-
于点N,连接AN,根据轴对称的性质得出AN=BN,并且根据三角形三边关系定理得出此时d=|AN-CN|=|BN-CN|=BC最大.运用待定系数法求出直线BC的解析式,再将x=-
代入,求出y的值,得到点N的坐标,然后利用勾股定理求出d的最大值BC即可.
| 3 |
| 2 |
| 3 |
| 2 |
解答: 解:在抛物线对称轴上存在一点N,能够使d=|AN-CN|的值最大.理由如下:
解:在抛物线对称轴上存在一点N,能够使d=|AN-CN|的值最大.理由如下:
∵y=-
x2-
x+2与x轴交于点A和点B,
∴点A和点B关于抛物线的对称轴对称,C(0,2),
令y=0,则0=-
x2-
x+2,
解得x=3或x=-6,
∴A(-6,0),B(3,0),
∵y=-
x2-
x+2=-
(x2+3x)+2=-
(x+
)2+
,
∴对称轴x=-
连接BC并延长,交直线x=-
于点N,连接AN,则AN=BN,此时d=|AN-CN|=|BN-CN|=BC最大.
设直线BC的解析式为y=mx+t,将B(3,0),C(0,2)两点的坐标代入,
得
,解得
,
∴直线BC的解析式为y=-
x+2,
当x=-
时,y=-
×(-
)+2=3,
∴点N的坐标为(-
,3),d的最大值为BC=
=
.
 解:在抛物线对称轴上存在一点N,能够使d=|AN-CN|的值最大.理由如下:
解:在抛物线对称轴上存在一点N,能够使d=|AN-CN|的值最大.理由如下:∵y=-
| 1 |
| 9 |
| 1 |
| 3 |
∴点A和点B关于抛物线的对称轴对称,C(0,2),
令y=0,则0=-
| 1 |
| 9 |
| 1 |
| 3 |
解得x=3或x=-6,
∴A(-6,0),B(3,0),
∵y=-
| 1 |
| 9 |
| 1 |
| 3 |
| 1 |
| 9 |
| 1 |
| 9 |
| 3 |
| 2 |
| 9 |
| 4 |
∴对称轴x=-
| 3 |
| 2 |
连接BC并延长,交直线x=-
| 3 |
| 2 |
设直线BC的解析式为y=mx+t,将B(3,0),C(0,2)两点的坐标代入,
得
|
|
∴直线BC的解析式为y=-
| 2 |
| 3 |
当x=-
| 3 |
| 2 |
| 2 |
| 3 |
| 3 |
| 2 |
∴点N的坐标为(-
| 3 |
| 2 |
| 32+22 |
| 13 |
点评:本题是二次函数的综合题型,其中涉及到运用待定系数法求一次函数、二次函数的解析式,抛物线与x轴的交点、轴对称的性质等知识,难度适中.其中根据轴对称及三角形三边关系定理确定点N的位置是关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
 如图所示,a∥b,∠1=158°,∠2=42°,∠4=50°.那么∠3=( )
如图所示,a∥b,∠1=158°,∠2=42°,∠4=50°.那么∠3=( )| A、50° | B、60° |
| C、70° | D、80° |

 如图,有一块含有45°角的直角三角板的两个锐角顶点放在直尺的对边上.如果∠1=22°,那么∠2的度数是
如图,有一块含有45°角的直角三角板的两个锐角顶点放在直尺的对边上.如果∠1=22°,那么∠2的度数是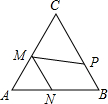 如图,在等边△ABC中,AB=4,P、M、N分别是BC,CA、AB边上动点,则PM+MN的最小值是
如图,在等边△ABC中,AB=4,P、M、N分别是BC,CA、AB边上动点,则PM+MN的最小值是
 如图,A为直线y=x上一点,AB⊥x轴于B点,双曲线y=
如图,A为直线y=x上一点,AB⊥x轴于B点,双曲线y=