题目内容
如图,AB=CD,AD=CB,那么下列结论中错误的是( )
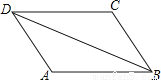
A. ∠A=∠C B. AB=AD C. AD∥BC D. AB∥CD
 B
【解析】∵在△ABD和△CDB中,
,
∴△ABD≌△CDB,
∴∠ADB=∠CBD,∠ABD=∠CDB,∠A=∠C
∴AD∥BC,AB∥CD,
∴A、C、D选项正确.
故选:B.
B
【解析】∵在△ABD和△CDB中,
,
∴△ABD≌△CDB,
∴∠ADB=∠CBD,∠ABD=∠CDB,∠A=∠C
∴AD∥BC,AB∥CD,
∴A、C、D选项正确.
故选:B.
练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
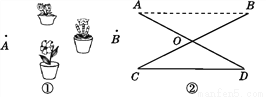
若 是关于
是关于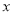 的方程
的方程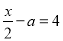 的解,则
的解,则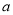 的值为( )
的值为( )
A. -6 B. 2 C. 16 D. -2
 D
【解析】把代入方程得:2-a=4,解得:a=-2,
故选D.
D
【解析】把代入方程得:2-a=4,解得:a=-2,
故选D. 在△ABC中,AB=AC,BC=12,∠B=30°,AB的垂直平分线DE交BC边于点E,AC的垂直平分线MN交BC于点N.
(1)求△AEN的周长;
(2)求证:BE=EN=NC.
 (1)12;(2)见解析
【解析】试题分析:(1)根据线段的垂直平分线的性质得到EB=EA,NA=NC,根据三角形的周长公式计算即可;
(2)根据等腰三角形的性质和三角形的外角的性质证明△AEN是等边三角形,等量代换证明即可.
试题解析:(1)∵DE是AB的垂直平分线,
∴EB=EA,
∵MN是AC的垂直平分线,
∴NA=NC,
则△AEN的周长=AE+A...
(1)12;(2)见解析
【解析】试题分析:(1)根据线段的垂直平分线的性质得到EB=EA,NA=NC,根据三角形的周长公式计算即可;
(2)根据等腰三角形的性质和三角形的外角的性质证明△AEN是等边三角形,等量代换证明即可.
试题解析:(1)∵DE是AB的垂直平分线,
∴EB=EA,
∵MN是AC的垂直平分线,
∴NA=NC,
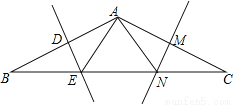
则△AEN的周长=AE+A... 教室里有几盆花,如图①,要想测量这几盆花两旁的A,B两点间的距离不方便,因此,选点A,B都能到达的一点O,如图②,连接BO并延长BO到点C,使CO=BO,连接AO并延长AO到点D,使DO=AO.那么C,D两点间的距离就是A,B两点间的距离.
理由:在△COD和△BOA中,  所以△COD≌△BOA( ).所以CD= .所以只要测出C,D两点间的距离就可知A,B两点间的距离.
所以△COD≌△BOA( ).所以CD= .所以只要测出C,D两点间的距离就可知A,B两点间的距离.
 SAS;BA
【解析】试题解析:在△COD和△BOA中,
所以△COD≌△BOA(SAS).
所以CD=BA.
故答案为:SAS;BA
SAS;BA
【解析】试题解析:在△COD和△BOA中,
所以△COD≌△BOA(SAS).
所以CD=BA.
故答案为:SAS;BA 已知在△ABC中,∠ABC=∠ACB,∠1=∠2,求证:AD平分∠BAC。
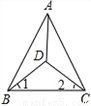
 证明见解析
【解析】试题分析:易证AB=AC和BD=CD,即可证明△ABD≌△ACD,可得∠BAD=∠CAD,即可解题.
试题解析:∵∠ABC=∠ACB,
∴AB=AC,
∵∠1=∠2,
∴BD=CD,
在△ABD和△ACD中,
,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,
∴AD平分∠BAC.
证明见解析
【解析】试题分析:易证AB=AC和BD=CD,即可证明△ABD≌△ACD,可得∠BAD=∠CAD,即可解题.
试题解析:∵∠ABC=∠ACB,
∴AB=AC,
∵∠1=∠2,
∴BD=CD,
在△ABD和△ACD中,
,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,
∴AD平分∠BAC. 如图,已知△ABE≌△ACD,且AB=AC.
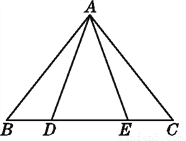
(1)说明△ABE经过怎样的变换后可与△ACD重合.
(2)∠BAD与∠CAE有何关系?请说明理由.
(3)BD与CE相等吗?为什么?
 (1)见解析;(2)∠BAD=∠CAE;(3)相等
【解析】试题分析:(1)由几何变换的类型说明即可,
(2)由三角形全等的性质求解即可,
(3)由三角形全等的性质求解即可.
试题解析: (1)△ABE先水平翻转,再平移即可与△ACD重合;
(2)∠BAD=∠CAE.
∵△ABE≌△ACD,
∴∠BAE=∠CAD,
∴∠BAE?∠DAE=∠CAD?∠...
(1)见解析;(2)∠BAD=∠CAE;(3)相等
【解析】试题分析:(1)由几何变换的类型说明即可,
(2)由三角形全等的性质求解即可,
(3)由三角形全等的性质求解即可.
试题解析: (1)△ABE先水平翻转,再平移即可与△ACD重合;
(2)∠BAD=∠CAE.
∵△ABE≌△ACD,
∴∠BAE=∠CAD,
∴∠BAE?∠DAE=∠CAD?∠... 如图所示,D,E分别是△ABC的边AC.BC上的点,若△ADB≌△EDB≌△EDC,则∠C的度数为 ( )
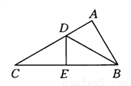
A. 15° B. 20° C. 25° D. 30°
 D
【解析】∵△ADB≌△EDB≌△EDC,
∴∠C=∠DBE=∠DBA,∠DEC=∠DEB=∠A=90°,
∴∠C=30°
故选D.
D
【解析】∵△ADB≌△EDB≌△EDC,
∴∠C=∠DBE=∠DBA,∠DEC=∠DEB=∠A=90°,
∴∠C=30°
故选D. 如图,已知△ABC中,AD是BC边上的高,点E在线段BD上,且AE平分∠BAC,若∠B=40°,∠C=78°,则∠EAD=__°.
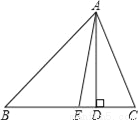
 19
【解析】试题分析:根据三角形内角和定理称求得∠BAC,再由AE平分∠BAC,可求得∠EAC,最后由∠ADC=90°,∠C=78°,可求得∠DAC,即∠EAD可求.
19
【解析】试题分析:根据三角形内角和定理称求得∠BAC,再由AE平分∠BAC,可求得∠EAC,最后由∠ADC=90°,∠C=78°,可求得∠DAC,即∠EAD可求.