题目内容
如图，在△ABC中，DE是边AB的垂直平分线，BC=8cm，AC=5cm，则△ADC的周长为（ ）
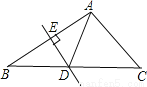
A. 14cm B. 13cm C. 11cm D. 9cm
B
【解析】试题解析：∵DE是边AB的垂直平分线
∴BD=AD
∴△ADC的周长为AC+DC+AD=AC+BC=5+8=13cm．
故选B.
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案下列图标是由我们熟悉的一些基本数学图形组成的,其中是轴对称图形的是__________.(填序号)
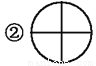
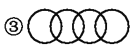
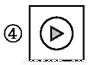
①②③④
【解析】①是轴对称图形，②是轴对称图形，③是轴对称图形，④是轴对称图形，
故答案为：①②③④. 如图,在四边形ABCD中,连接AC,BD,若要使AB∥CD,则需要添加的条件是( )
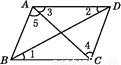
A. ∠1=∠2 B. ∠2=∠3 C. ∠3=∠4 D. ∠4=∠5
D
【解析】A、当∠1=∠2时, AD∥BC ,故此选项错误;
B、当∠2=∠3时,无法得到AB∥CD,故此选项错误;
C、当∠3=∠4时,无法得到AB∥CD,故此选项错误;
D、当∠4=∠5时, AB∥CD,故此选项正确.
故选D. 如图,在四边形ABCD中,连接AC,BD,若要使AB∥CD,则需要添加的条件是( )
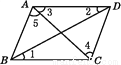
A. ∠1=∠2 B. ∠2=∠3 C. ∠3=∠4 D. ∠4=∠5
D
【解析】A、当∠1=∠2时, AD∥BC ,故此选项错误;
B、当∠2=∠3时,无法得到AB∥CD,故此选项错误;
C、当∠3=∠4时,无法得到AB∥CD,故此选项错误;
D、当∠4=∠5时, AB∥CD,故此选项正确.
故选D. 在△ABC中，AB=AC，BC=12，∠B=30°，AB的垂直平分线DE交BC边于点E，AC的垂直平分线MN交BC于点N.
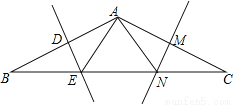
（1）求△AEN的周长；
（2）求证：BE=EN=NC.
（1）12；（2）见解析
【解析】试题分析：（1）根据线段的垂直平分线的性质得到EB=EA，NA=NC，根据三角形的周长公式计算即可；
（2）根据等腰三角形的性质和三角形的外角的性质证明△AEN是等边三角形，等量代换证明即可．
试题解析：（1）∵DE是AB的垂直平分线，
∴EB=EA，
∵MN是AC的垂直平分线，
∴NA=NC，
则△AEN的周长=AE+A... 如图,AB=DC,∠A=∠D.试说明:∠ABC=∠DCB.
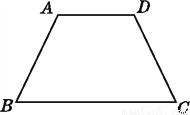
说明见解析.
【解析】试题分析：连接AC、BD，利用“边角边”证明△ABD和△DCA全等，根据全等三角形对应边相等可得AC=BD，再利用“边边边”证明△ABC和△DCB全等，根据全等三角形对应角相等证明即可．
试题解析：证明：如图，连接AC、BD，
在△ABD和△DCA中，
，
∴△ABD≌△DCA（SAS），
∴AC=BD，
在△ABC和△DCB中，
... 教室里有几盆花,如图①,要想测量这几盆花两旁的A,B两点间的距离不方便,因此,选点A,B都能到达的一点O,如图②,连接BO并延长BO到点C,使CO=BO,连接AO并延长AO到点D,使DO=AO.那么C,D两点间的距离就是A,B两点间的距离.
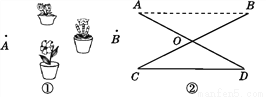
理由:在△COD和△BOA中, 
所以△COD≌△BOA( ).所以CD= .所以只要测出C,D两点间的距离就可知A,B两点间的距离.
SAS;BA
【解析】试题解析：在△COD和△BOA中,
所以△COD≌△BOA(SAS).
所以CD=BA.
故答案为：SAS;BA 如图,已知△ABE≌△ACD,且AB=AC.
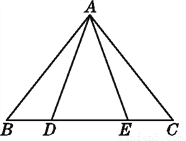
(1)说明△ABE经过怎样的变换后可与△ACD重合.
(2)∠BAD与∠CAE有何关系?请说明理由.
(3)BD与CE相等吗?为什么?
（1）见解析；（2）∠BAD=∠CAE；（3）相等
【解析】试题分析：（1）由几何变换的类型说明即可，
（2）由三角形全等的性质求解即可，
（3）由三角形全等的性质求解即可．
试题解析: (1)△ABE先水平翻转，再平移即可与△ACD重合；
(2)∠BAD=∠CAE.
∵△ABE≌△ACD，
∴∠BAE=∠CAD，
∴∠BAE?∠DAE=∠CAD?∠... 已知a是－2的相反数，且|b＋1|＝0，则[－3a2(ab2＋2a)＋4a(－ab)2]÷(－4a)的值为_____.
5
【解析】[－3a2(ab2＋2a)＋4a(－ab)2]÷(－4a)
=
=
=
∵a是－2的相反数，且|b＋1|＝0，
∴a=2，b=-1，
∴原式==-1+6=5.