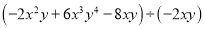题目内容
已知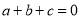
， 
.
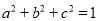（1）求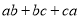
的值；
（2）求
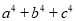的值．
（1） （2）
【解析】试题分析：（1）把a+b+c=0两边平方，然后利用代入法等量代换即可；
（2）把ab+bc+ca与两边分别乘方即可.
试题解析：（1）因为a+b+c=0
所以+2ab+2ac+2bc=0
∴2ab+2ac+2bc=-1
即ab+bc+ca=-
（2）因为a+b+c=0，a2+b2+c2=1
所以+2ab+2ac+2bc=0
...
练习册系列答案
相关题目
在△ABC中，AB=AC，BC=12，∠B=30°，AB的垂直平分线DE交BC边于点E，AC的垂直平分线MN交BC于点N.
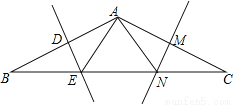
（1）求△AEN的周长；
（2）求证：BE=EN=NC.
（1）12；（2）见解析
【解析】试题分析：（1）根据线段的垂直平分线的性质得到EB=EA，NA=NC，根据三角形的周长公式计算即可；
（2）根据等腰三角形的性质和三角形的外角的性质证明△AEN是等边三角形，等量代换证明即可．
试题解析：（1）∵DE是AB的垂直平分线，
∴EB=EA，
∵MN是AC的垂直平分线，
∴NA=NC，
则△AEN的周长=AE+A... 如图所示，D，E分别是△ABC的边AC．BC上的点，若△ADB≌△EDB≌△EDC，则∠C的度数为 （ ）
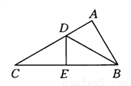
A. 15° B. 20° C. 25° D. 30°
D
【解析】∵△ADB≌△EDB≌△EDC，
∴∠C=∠DBE=∠DBA，∠DEC=∠DEB=∠A=90°，
∴∠C=30°
故选D. 如图，已知△ABC中，AD是BC边上的高，点E在线段BD上，且AE平分∠BAC，若∠B=40°，∠C=78°，则∠EAD=__°．
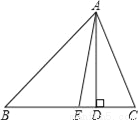
19
【解析】试题分析：根据三角形内角和定理称求得∠BAC，再由AE平分∠BAC，可求得∠EAC，最后由∠ADC=90°，∠C=78°，可求得∠DAC，即∠EAD可求. 如图，AB∥FC，DE＝EF，AB＝15，CF＝8，则BD等于( )
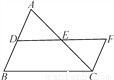
A. 8 B. 7 C. 6 D. 5
B
【解析】∵AB//CF，
∴∠A=∠ECF，
又∵DE=EF，∠AED=∠CEF，
∴△ADE≌△CFE，
∴AD=CF=8，
∴BD=AB-AD=15-8=7，
故选B. 已知a是－2的相反数，且|b＋1|＝0，则[－3a2(ab2＋2a)＋4a(－ab)2]÷(－4a)的值为_____.
5
【解析】[－3a2(ab2＋2a)＋4a(－ab)2]÷(－4a)
=
=
=
∵a是－2的相反数，且|b＋1|＝0，
∴a=2，b=-1，
∴原式==-1+6=5. 已知(x－2 015)2＋(x－2 017)2＝34，则(x－2 016)2的值是( )
A. 4 B. 8 C. 12 D. 16
D
【解析】(x－2 015)2＋(x－2 017)2
=(x－2 016+1)2＋(x－2 016-1)2
=
==34
∴
故选D. 
【解析】试题分析：利用多项式除以单项式的运算法则计算即可.
试题解析：
=
= 如图，数轴上有A、B、C、D四个整数点（即各点均表示整数），且3AB=BC=2CD．若A、D两点所表示的数分别是﹣6和5，则线段AC的中点所表示的数是（ ）
A. ﹣3 B. ﹣1 C. 3 D. ﹣2
D
【解析】首先设BC为6x，根据3AB=BC=2CD表示出AB=2x，CD=3x，然后根据线段AD的长度建立方程，进而求出点C所表示的数，再利用两点之间的中点公式即可得出答案．
【解析】
设BC=6x，
∵3AB=BC=2CD，
∴AB=2x，CD=3x，
∴AD=AB+BC+CD=11x，
∵A，D两点所表示的数分别是?6和5，
∴AD=11，
...