题目内容
如图,(1)如果∠1=__________,那么DE∥AC;(同位角相等,两直线平行);
(2)如果∠1=__________,那么EF∥BC;(内错角相等,两直线平行);
(3)如果∠DEF+__________=180°,那么DE∥AC;(同旁内角互补,两直线平行);
(4)如果∠2+__________=180°,那么AB∥DF;(同旁内角互补,两直线平行).
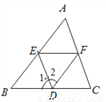
 ∠C; ∠DEF; ∠EFC; ∠AED.
【解析】(1)如果∠1=∠C ,那么DE//AC;(同位角相等,两直线平行)
(2)如果∠1=∠DEF ,那么EF//BC;(内错角相等,两直线平行)
(3)如果∠DEF+∠EFC =180°,那么DE//AC;(同旁内角互补,两直线平行)
(4)如果∠2+∠AED =180°,,那么AB//DF;(同旁内角互补,两直线平行)
...
∠C; ∠DEF; ∠EFC; ∠AED.
【解析】(1)如果∠1=∠C ,那么DE//AC;(同位角相等,两直线平行)
(2)如果∠1=∠DEF ,那么EF//BC;(内错角相等,两直线平行)
(3)如果∠DEF+∠EFC =180°,那么DE//AC;(同旁内角互补,两直线平行)
(4)如果∠2+∠AED =180°,,那么AB//DF;(同旁内角互补,两直线平行)
...
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案一个不透明袋子中有1个红球,1个绿球和n个白球,这些球除颜色外无其他差别.
(1)当n=1时,从袋中随机摸出1个球,摸到红球和摸到白球的可能性是否相同?
(2)从袋中随机摸出一个球,记录其颜色,然后放回.大量重复该试验,发现摸到绿球的频率稳定于0.25,求n的值.
 (1) 相同:(2)2.
【解析】分析:(1)n=1,袋子中有1个红球和1个白球,则从袋中随机摸出1个球,摸到红球与摸到白球的概率都为;(2)利用频率估计概率得到摸到红球的概率为0.25,则根据概率公式得到,然后解方程即可.
本题解析:
解:(1)当n=1时,袋中红球数量和白球数量相同,故摸到两种颜色的球的可能性相同.
(2)由题意得0.25=,即(2+n)×0.25=1,...
(1) 相同:(2)2.
【解析】分析:(1)n=1,袋子中有1个红球和1个白球,则从袋中随机摸出1个球,摸到红球与摸到白球的概率都为;(2)利用频率估计概率得到摸到红球的概率为0.25,则根据概率公式得到,然后解方程即可.
本题解析:
解:(1)当n=1时,袋中红球数量和白球数量相同,故摸到两种颜色的球的可能性相同.
(2)由题意得0.25=,即(2+n)×0.25=1,... 若 是关于
是关于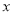 的方程
的方程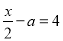 的解,则
的解,则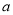 的值为( )
的值为( )
A. -6 B. 2 C. 16 D. -2
 D
【解析】把代入方程得:2-a=4,解得:a=-2,
故选D.
D
【解析】把代入方程得:2-a=4,解得:a=-2,
故选D. 如图,在四边形ABCD中,连接AC,BD,若要使AB∥CD,则需要添加的条件是( )
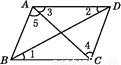
A. ∠1=∠2 B. ∠2=∠3 C. ∠3=∠4 D. ∠4=∠5
 D
【解析】A、当∠1=∠2时, AD∥BC ,故此选项错误;
B、当∠2=∠3时,无法得到AB∥CD,故此选项错误;
C、当∠3=∠4时,无法得到AB∥CD,故此选项错误;
D、当∠4=∠5时, AB∥CD,故此选项正确.
故选D.
D
【解析】A、当∠1=∠2时, AD∥BC ,故此选项错误;
B、当∠2=∠3时,无法得到AB∥CD,故此选项错误;
C、当∠3=∠4时,无法得到AB∥CD,故此选项错误;
D、当∠4=∠5时, AB∥CD,故此选项正确.
故选D. 如图,两只手的食指和大拇指在同一个平面内,它们构成的一对角可看成是___.
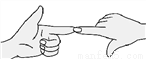
 内错角
【解析】图中两只手的食指和拇指构成”Z“形,根据内错角是在截线两旁,被截线之内的两角,内错角的边构成”Z“形,可知答案为:内错角.
故答案为:内错角.
内错角
【解析】图中两只手的食指和拇指构成”Z“形,根据内错角是在截线两旁,被截线之内的两角,内错角的边构成”Z“形,可知答案为:内错角.
故答案为:内错角. 如图,在四边形ABCD中,连接AC,BD,若要使AB∥CD,则需要添加的条件是( )
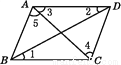
A. ∠1=∠2 B. ∠2=∠3 C. ∠3=∠4 D. ∠4=∠5
 D
【解析】A、当∠1=∠2时, AD∥BC ,故此选项错误;
B、当∠2=∠3时,无法得到AB∥CD,故此选项错误;
C、当∠3=∠4时,无法得到AB∥CD,故此选项错误;
D、当∠4=∠5时, AB∥CD,故此选项正确.
故选D.
D
【解析】A、当∠1=∠2时, AD∥BC ,故此选项错误;
B、当∠2=∠3时,无法得到AB∥CD,故此选项错误;
C、当∠3=∠4时,无法得到AB∥CD,故此选项错误;
D、当∠4=∠5时, AB∥CD,故此选项正确.
故选D. 在△ABC中,AB=AC,BC=12,∠B=30°,AB的垂直平分线DE交BC边于点E,AC的垂直平分线MN交BC于点N.
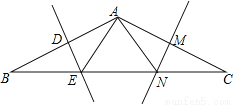
(1)求△AEN的周长;
(2)求证:BE=EN=NC.
 (1)12;(2)见解析
【解析】试题分析:(1)根据线段的垂直平分线的性质得到EB=EA,NA=NC,根据三角形的周长公式计算即可;
(2)根据等腰三角形的性质和三角形的外角的性质证明△AEN是等边三角形,等量代换证明即可.
试题解析:(1)∵DE是AB的垂直平分线,
∴EB=EA,
∵MN是AC的垂直平分线,
∴NA=NC,
则△AEN的周长=AE+A...
(1)12;(2)见解析
【解析】试题分析:(1)根据线段的垂直平分线的性质得到EB=EA,NA=NC,根据三角形的周长公式计算即可;
(2)根据等腰三角形的性质和三角形的外角的性质证明△AEN是等边三角形,等量代换证明即可.
试题解析:(1)∵DE是AB的垂直平分线,
∴EB=EA,
∵MN是AC的垂直平分线,
∴NA=NC,
则△AEN的周长=AE+A... 教室里有几盆花,如图①,要想测量这几盆花两旁的A,B两点间的距离不方便,因此,选点A,B都能到达的一点O,如图②,连接BO并延长BO到点C,使CO=BO,连接AO并延长AO到点D,使DO=AO.那么C,D两点间的距离就是A,B两点间的距离.
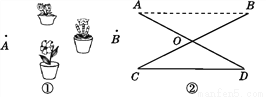
理由:在△COD和△BOA中,  所以△COD≌△BOA( ).所以CD= .所以只要测出C,D两点间的距离就可知A,B两点间的距离.
所以△COD≌△BOA( ).所以CD= .所以只要测出C,D两点间的距离就可知A,B两点间的距离.
 SAS;BA
【解析】试题解析:在△COD和△BOA中,
所以△COD≌△BOA(SAS).
所以CD=BA.
故答案为:SAS;BA
SAS;BA
【解析】试题解析:在△COD和△BOA中,
所以△COD≌△BOA(SAS).
所以CD=BA.
故答案为:SAS;BA 如图,已知△ABC中,AD是BC边上的高,点E在线段BD上,且AE平分∠BAC,若∠B=40°,∠C=78°,则∠EAD=__°.
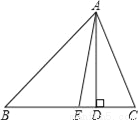
 19
【解析】试题分析:根据三角形内角和定理称求得∠BAC,再由AE平分∠BAC,可求得∠EAC,最后由∠ADC=90°,∠C=78°,可求得∠DAC,即∠EAD可求.
19
【解析】试题分析:根据三角形内角和定理称求得∠BAC,再由AE平分∠BAC,可求得∠EAC,最后由∠ADC=90°,∠C=78°,可求得∠DAC,即∠EAD可求. 
