题目内容
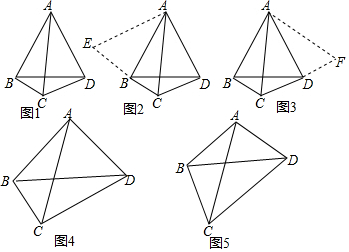
11.数学课上,张老师出示了问题:如图1,AC,BD是四边形ABCD的对角线,若∠ACB=∠ACD=∠ABD=∠ADB=60°,则线段BC,CD,AC三者之间有何等量关系?经过思考,小明展示了一种正确的思路:如图2,延长CB到E,使BE=CD,连接AE,证得△ABE≌△ADC,从而容易证明△ACE是等边三角形,故AC=CE,所以AC=BC+CD.
小亮展示了另一种正确的思路:如图3,将△ABC绕着点A逆时针旋转60°,使AB与AD重合,从而容易证明△ACF是等边三角形,故AC=CF,所以AC=BC+CD.
在此基础上,同学们作了进一步的研究:
(1)小颖提出:如图4,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=45°”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小颖提出的问题,请你写出结论,并给出证明.
(2)小华提出:如图5,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=α”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小华提出的问题,请你写出结论,不用证明.
分析 (1)先判断出∠ADE=∠ABC,即可得出△ACE是等腰三角形,再得出∠AEC=45°,即可得出等腰直角三角形,即可;(判断∠ADE=∠ABC也可以先判断出点A,B,C,D四点共圆)
(2)先判断出∠ADE=∠ABC,即可得出△ACE是等腰三角形,再用三角函数即可得出结论.
解答 解:(1)BC+CD=$\sqrt{2}$AC;
理由:如图1,
延长CD至E,使DE=BC,
∵∠ABD=∠ADB=45°,
∴AB=AD,∠BAD=180°-∠ABD-∠ADB=90°,
∵∠ACB=∠ACD=45°,
∴∠ACB+∠ACD=90°,
∴∠BAD+∠BCD=180°,
∴∠ABC+∠ADC=180°,
∵∠ADC+∠ADE=180°,
∴∠ABC=∠ADE,
在△ABC和△ADE中,$\left\{\begin{array}{l}{AB=AD}\\{∠ABC=∠ADE}\\{BC=DE}\end{array}\right.$,
∴△ABC≌△ADE(SAS),
∴∠ACB=∠AED=45°,AC=AE,
∴△ACE是等腰直角三角形,
∴CE=$\sqrt{2}$AC,
∵CE=CD+DE=CD+BC,
∴BC+CD=$\sqrt{2}$AC;
(2)BC+CD=2AC•cosα.理由:如图2,
延长CD至E,使DE=BC,
∵∠ABD=∠ADB=α,
∴AB=AD,∠BAD=180°-∠ABD-∠ADB=180°-2α,
∵∠ACB=∠ACD=α,
∴∠ACB+∠ACD=2α,
∴∠BAD+∠BCD=180°,
∴∠ABC+∠ADC=180°,
∵∠ADC+∠ADE=180°,
∴∠ABC=∠ADE,
在△ABC和△ADE中,$\left\{\begin{array}{l}{AB=AD}\\{∠ABC=∠ADE}\\{BC=DE}\end{array}\right.$,
∴△ABC≌△ADE(SAS),
∴∠ACB=∠AED=α,AC=AE,
∴∠AEC=α,
过点A作AF⊥CE于F,
∴CE=2CF,在Rt△ACF中,∠ACD=α,CF=AC•cos∠ACD=AC•cosα,
∴CE=2CF=2AC•cosα,
∵CE=CD+DE=CD+BC,
∴BC+CD=2AC•cosα.
点评 此题是几何变换综合题,主要考查了全等三角形的判定,四边形的内角和,等腰三角形的判定和性质,解本题的关键是构造全等三角形,是一道综合性较强的题目.

| A. | $\frac{5}{13}$ | B. | $\frac{12}{13}$ | C. | $\frac{5}{12}$ | D. | $\frac{12}{5}$ |
 某景区修建一栋复古建筑,其窗户设计如图所示.圆O的圆心与矩形ABCD对角线的交点重合,且圆与矩形上下两边相切(E为上切点),与左右两边相交(F,G为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1m,根据设计要求,若∠EOF=45°,则此窗户的透光率(透光区域与矩形窗面的面积的比值)为$\frac{(π+2)\sqrt{2}}{8}$.
某景区修建一栋复古建筑,其窗户设计如图所示.圆O的圆心与矩形ABCD对角线的交点重合,且圆与矩形上下两边相切(E为上切点),与左右两边相交(F,G为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1m,根据设计要求,若∠EOF=45°,则此窗户的透光率(透光区域与矩形窗面的面积的比值)为$\frac{(π+2)\sqrt{2}}{8}$.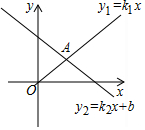 如图,正比例函数y1=k1x和一次函数y2=k2x+b的图象相交于点A(2,1),当x<2时,y1<y2.(填“>”或“<”).
如图,正比例函数y1=k1x和一次函数y2=k2x+b的图象相交于点A(2,1),当x<2时,y1<y2.(填“>”或“<”).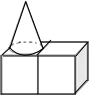 如图,是由两个相同的小正方体和一个圆锥体组成的立体图形,画出实物的三视图.
如图,是由两个相同的小正方体和一个圆锥体组成的立体图形,画出实物的三视图.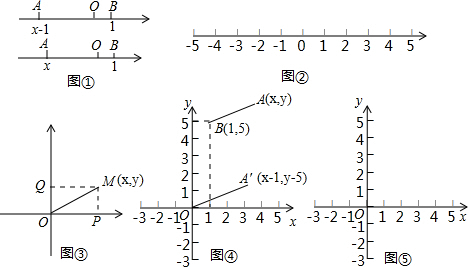
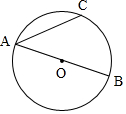 如图,AB是⊙O的直径,$\widehat{AC}$=$\widehat{BC}$,AB=2,连接AC.
如图,AB是⊙O的直径,$\widehat{AC}$=$\widehat{BC}$,AB=2,连接AC.