题目内容
1.在Rt△ABC中,∠C=90°,AB=13,AC=5,则sinA的值为( )| A. | $\frac{5}{13}$ | B. | $\frac{12}{13}$ | C. | $\frac{5}{12}$ | D. | $\frac{12}{5}$ |
分析 根据勾股定理求出BC,根据正弦的概念计算即可.
解答 解:在Rt△ABC中,由勾股定理得,BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=12,
∴sinA=$\frac{BC}{AB}$=$\frac{12}{13}$,
故选:B.
点评 本题考查的是锐角三角函数的定义,掌握锐角A的对边a与斜边c的比叫做∠A的正弦是解题的关键.

练习册系列答案
相关题目
12.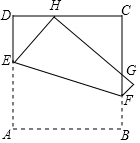 如图,将正方形ABCD折叠,使顶点A与CD边上的一点H重合(H不与端点C,D重合),折痕交AD于点E,交BC于点F,边AB折叠后与边BC交于点G.设正方形ABCD的周长为m,△CHG的周长为n,则$\frac{n}{m}$的值为( )
如图,将正方形ABCD折叠,使顶点A与CD边上的一点H重合(H不与端点C,D重合),折痕交AD于点E,交BC于点F,边AB折叠后与边BC交于点G.设正方形ABCD的周长为m,△CHG的周长为n,则$\frac{n}{m}$的值为( )
 如图,将正方形ABCD折叠,使顶点A与CD边上的一点H重合(H不与端点C,D重合),折痕交AD于点E,交BC于点F,边AB折叠后与边BC交于点G.设正方形ABCD的周长为m,△CHG的周长为n,则$\frac{n}{m}$的值为( )
如图,将正方形ABCD折叠,使顶点A与CD边上的一点H重合(H不与端点C,D重合),折痕交AD于点E,交BC于点F,边AB折叠后与边BC交于点G.设正方形ABCD的周长为m,△CHG的周长为n,则$\frac{n}{m}$的值为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{1}{2}$ | ||
| C. | $\frac{\sqrt{5}-1}{2}$ | D. | 随H点位置的变化而变化 |
9.在国家“一带一路”战略下,我国与欧洲开通了互利互惠的中欧班列.行程最长,途经城市和国家最多的一趟专列全程长13000km,将13000用科学记数法表示应为( )
| A. | 0.13×105 | B. | 1.3×104 | C. | 1.3×105 | D. | 13×103 |
6.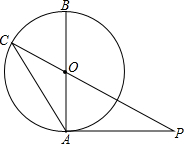 如图,AB是⊙O的直径,PA切⊙O于点A,连结PO并延长交⊙O于点C,连结AC,AB=10,∠P=30°,则AC的长度是( )
如图,AB是⊙O的直径,PA切⊙O于点A,连结PO并延长交⊙O于点C,连结AC,AB=10,∠P=30°,则AC的长度是( )
 如图,AB是⊙O的直径,PA切⊙O于点A,连结PO并延长交⊙O于点C,连结AC,AB=10,∠P=30°,则AC的长度是( )
如图,AB是⊙O的直径,PA切⊙O于点A,连结PO并延长交⊙O于点C,连结AC,AB=10,∠P=30°,则AC的长度是( )| A. | $5\sqrt{3}$ | B. | $5\sqrt{2}$ | C. | 5 | D. | $\frac{5}{2}$ |
13.-5的倒数是( )
| A. | -5 | B. | 5 | C. | $\frac{1}{5}$ | D. | $-\frac{1}{5}$ |
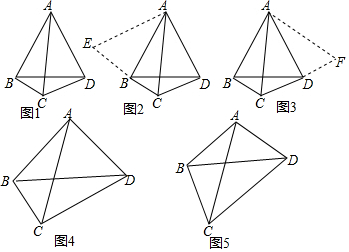
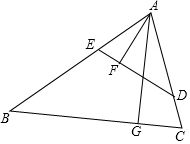 如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.