题目内容
20.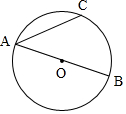 如图,AB是⊙O的直径,$\widehat{AC}$=$\widehat{BC}$,AB=2,连接AC.
如图,AB是⊙O的直径,$\widehat{AC}$=$\widehat{BC}$,AB=2,连接AC.(1)求证:∠CAB=45°;
(2)若直线l为⊙O的切线,C是切点,在直线l上取一点D,使BD=AB,BD所在的直线与AC所在的直线相交于点E,连接AD.
①试探究AE与AD之间的是数量关系,并证明你的结论;
②$\frac{EB}{CD}$是否为定值?若是,请求出这个定值;若不是,请说明理由.
分析 (1)由AB是⊙O的直径知∠ACB=90°,由$\widehat{AC}$=$\widehat{BC}$即AC=BC可得答案;
(2)分∠ABD为锐角和钝角两种情况,①作BF⊥l于点F,证四边形OBFC是矩形可得AB=2OC=2BF,结合BD=AB知∠BDF=30°,再求出∠BDA和∠DEA度数可得;②同理BF=$\frac{1}{2}$BD,即可知∠BDC=30°,分别求出∠BEC、∠ADB即可得;
(3)分D在C左侧和点D在点C右侧两种情况,作EI⊥AB,证△CAD∽△BAE得$\frac{AC}{BA}$=$\frac{CD}{AE}$=$\frac{1}{\sqrt{2}}$,即AE=$\sqrt{2}$CD,结合EI=$\frac{1}{2}$BE、EI=$\frac{\sqrt{2}}{2}$AE,可得BE=2EI=2×$\frac{\sqrt{2}}{2}$AE=$\sqrt{2}$AE=$\sqrt{2}$×$\sqrt{2}$CD=2CD,从而得出结论.
解答 解:(1)如图1,连接BC,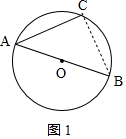
∵AB是⊙O的直径,
∴∠ACB=90°,
∵AC=BC,
∴∠CAB=∠CBA=$\frac{180°-90°}{2}$=45°;
(2)①当∠ABD为锐角时,如图2所示,作BF⊥l于点F,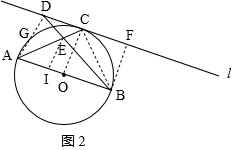
由(1)知△ACB是等腰直角三角形,
∵OA=OB=OC,
∴△BOC为等腰直角三角形,
∵l是⊙O的切线,
∴OC⊥l,
又BF⊥l,
∴四边形OBFC是矩形,
∴AB=2OC=2BF,
∵BD=AB,
∴BD=2BF,
∴∠BDF=30°,
∴∠DBA=30°,∠BDA=∠BAD=75°,
∴∠CBE=∠CBA-∠DBA=45°-30°=15°,
∴∠DEA=∠CEB=90°-∠CBE=75°,
∴∠ADE=∠AED,
∴AD=AE;
②当∠ABD为钝角时,如图3所示,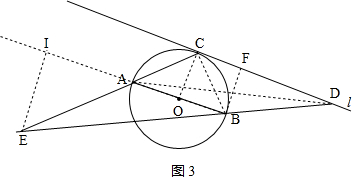
同理可得BF=$\frac{1}{2}$BD,即可知∠BDC=30°,
∵OC⊥AB、OC⊥直线l,
∴AB∥直线l,
∴∠ABD=150°,∠ABE=30°,
∴∠BEC=90°-(∠ABE+∠ABC)=90°-(30°+45°)=15°,
∵AB=DB,
∴∠ADB=$\frac{1}{2}$∠ABE=15°,
∴∠BEC=∠ADE,
∴AE=AD;
(3)①如图2,当D在C左侧时,
由(2)知CD∥AB,∠ACD=∠BAE,∠DAC=∠EBA=30°,
∴△CAD∽△BAE,
∴$\frac{AC}{BA}$=$\frac{CD}{AE}$=$\frac{1}{\sqrt{2}}$,
∴AE=$\sqrt{2}$CD,
作EI⊥AB于点I,
∵∠CAB=45°、∠ABD=30°,
∴BE=2EI=2×$\frac{\sqrt{2}}{2}$AE=$\sqrt{2}$AE=$\sqrt{2}$×$\sqrt{2}$CD=2CD,
∴$\frac{BE}{CD}$=2;
②如图3,当点D在点C右侧时,过点E作EI⊥AB于I,
由(2)知∠ADC=∠BEA=15°,
∵AB∥CD,
∴∠EAB=∠ACD,
∴△ACD∽△BAE,
∴$\frac{AC}{BA}$=$\frac{CD}{AE}$=$\frac{1}{\sqrt{2}}$,
∴$AE=\sqrt{2}$CD,
∵BA=BD,∠BAD=∠BDA=15°,
∴∠IBE=30°,
∴BE=2EI=2×$\frac{\sqrt{2}}{2}$AE=$\sqrt{2}$AE=$\sqrt{2}$×$\sqrt{2}$CD=2CD,
∴$\frac{BE}{CD}$=2.
点评 本题主要考查圆的综合问题,熟练掌握切线的性质、等腰直角三角形的判定与性质、圆心角定理及相似三角形的判定与性质是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
| A. |  | B. |  | C. |  | D. |  |
| A. | 8a-a=8 | B. | a3•a2=a6 | C. | (-a)4=a4 | D. | (a-b)2=a2-b2 |
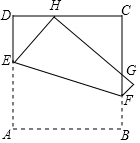 如图,将正方形ABCD折叠,使顶点A与CD边上的一点H重合(H不与端点C,D重合),折痕交AD于点E,交BC于点F,边AB折叠后与边BC交于点G.设正方形ABCD的周长为m,△CHG的周长为n,则$\frac{n}{m}$的值为( )
如图,将正方形ABCD折叠,使顶点A与CD边上的一点H重合(H不与端点C,D重合),折痕交AD于点E,交BC于点F,边AB折叠后与边BC交于点G.设正方形ABCD的周长为m,△CHG的周长为n,则$\frac{n}{m}$的值为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{1}{2}$ | ||
| C. | $\frac{\sqrt{5}-1}{2}$ | D. | 随H点位置的变化而变化 |
| A. | 0.13×105 | B. | 1.3×104 | C. | 1.3×105 | D. | 13×103 |
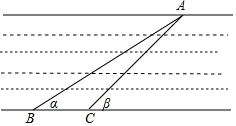 如图,为了测量某条河的宽度,现在河边的一岸边任意取一点A,又在河的另一岸边去两点B、C测得∠α=30°,∠β=45°,量得BC长为100米.求河的宽度(结果保留根号).
如图,为了测量某条河的宽度,现在河边的一岸边任意取一点A,又在河的另一岸边去两点B、C测得∠α=30°,∠β=45°,量得BC长为100米.求河的宽度(结果保留根号).