题目内容
16.下列关于函数y=x2-6x+10的四个命题:①当x=0时,y有最小值10;
②n为任意实数,x=3+n时的函数值大于x=3-n时的函数值;
③若n>3,且n是整数,当n≤x≤n+1时,y的整数值有(2n-4)个;
④若函数图象过点(a,y0)和(b,y0+1),其中a>0,b>0,则a<b.
其中真命题的序号是( )
| A. | ① | B. | ② | C. | ③ | D. | ④ |
分析 分别根据二次函数的图象与系数的关系、抛物线的顶点坐标公式及抛物线的增减性对各选项进行逐一分析.
解答 解:∵y=x2-6x+10=(x-3)2+1,
∴当x=3时,y有最小值1,故①错误;
当x=3+n时,y=(3+n)2-6(3+n)+10,
当x=3-n时,y=(n-3)2-6(n-3)+10,
∵(3+n)2-6(3+n)+10-[(n-3)2-6(n-3)+10]=0,
∴n为任意实数,x=3+n时的函数值等于x=3-n时的函数值,故②错误;
∵抛物线y=x2-6x+10的对称轴为x=3,a=1>0,
∴当x>3时,y随x的增大而增大,
当x=n+1时,y=(n+1)2-6(n+1)+10,
当x=n时,y=n2-6n+10,
(n+1)2-6(n+1)+10-[n2-6n+10]=2n-4,
∵n是整数,
∴2n-4是整数,故③正确;
∵抛物线y=x2-6x+10的对称轴为x=3,1>0,
∴当x>3时,y随x的增大而增大,x<0时,y随x的增大而减小,
∵y0+1>y0,∴当0<a<3,0<b<3时,a>b,当a>3,b>3时,a<b,当0<a<3,b>3时,a<b,当0<a<3,b>3时,a<b,故④是假命题.故选C.
点评 本题主要考查了二次函数的意义,性质,图象,能够根据二次函数的性质数形结合是解决问题的关键.

练习册系列答案
相关题目
4.下列运算中,结果正确的是( )
| A. | (a3)2=a6 | B. | (ab)3=a3b | C. | a•a3=a3 | D. | a8÷a4=a2 |
1.下列各式计算正确的是( )
| A. | (b+2a)(2a-b)=b2-4a2 | B. | 2a3+a3=3a6 | C. | a3•a=a4 | D. | (-a2b)3=a6b3 |
5.下列计算结果正确的是( )
| A. | 8a-a=8 | B. | a3•a2=a6 | C. | (-a)4=a4 | D. | (a-b)2=a2-b2 |
6.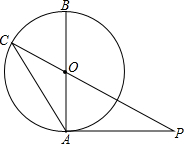 如图,AB是⊙O的直径,PA切⊙O于点A,连结PO并延长交⊙O于点C,连结AC,AB=10,∠P=30°,则AC的长度是( )
如图,AB是⊙O的直径,PA切⊙O于点A,连结PO并延长交⊙O于点C,连结AC,AB=10,∠P=30°,则AC的长度是( )
 如图,AB是⊙O的直径,PA切⊙O于点A,连结PO并延长交⊙O于点C,连结AC,AB=10,∠P=30°,则AC的长度是( )
如图,AB是⊙O的直径,PA切⊙O于点A,连结PO并延长交⊙O于点C,连结AC,AB=10,∠P=30°,则AC的长度是( )| A. | $5\sqrt{3}$ | B. | $5\sqrt{2}$ | C. | 5 | D. | $\frac{5}{2}$ |
 在数轴上,点A表示1,现将点A沿x轴做如下移动,第一次点A向左移动3个单位长度到达点A1,第二次将点A1向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,则A3表示的数是-5按照这种移动规律移动下去,第n次移动到点AN,如果点AN与原点的距离不小于20,那么n的最小值是13.
在数轴上,点A表示1,现将点A沿x轴做如下移动,第一次点A向左移动3个单位长度到达点A1,第二次将点A1向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,则A3表示的数是-5按照这种移动规律移动下去,第n次移动到点AN,如果点AN与原点的距离不小于20,那么n的最小值是13.
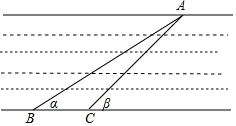 如图,为了测量某条河的宽度,现在河边的一岸边任意取一点A,又在河的另一岸边去两点B、C测得∠α=30°,∠β=45°,量得BC长为100米.求河的宽度(结果保留根号).
如图,为了测量某条河的宽度,现在河边的一岸边任意取一点A,又在河的另一岸边去两点B、C测得∠α=30°,∠β=45°,量得BC长为100米.求河的宽度(结果保留根号).