题目内容
9.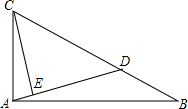 如图,已知点D是Rt△ABC的斜边BC上的一点,tanB=$\frac{1}{2}$,BC=3BD,CE⊥AD,则$\frac{AE}{CE}$=$\frac{1}{4}$.
如图,已知点D是Rt△ABC的斜边BC上的一点,tanB=$\frac{1}{2}$,BC=3BD,CE⊥AD,则$\frac{AE}{CE}$=$\frac{1}{4}$.
分析 根据题意结合平行线的性质得出$\frac{BD}{DC}$=$\frac{BF}{AF}$的值,进而利用锐角三角函数关系得出tan∠ACE=tan∠DAF=$\frac{AE}{EC}=\frac{DF}{AF}$的值,问题得解.
解答  解:过点D作DF⊥AB于点F,
解:过点D作DF⊥AB于点F,
∵∠CAB=90°,DF⊥AB,
∴AC∥DF,
∴$\frac{BD}{DC}$=$\frac{BF}{AF}$=
∵BC=3BD,
∴$\frac{BD}{DC}$=$\frac{BF}{AF}$=$\frac{1}{2}$,
∴AF=k•BF
∵tanB=$\frac{1}{2}$,
∴$\frac{DF}{FB}$=$\frac{1}{2}$,
∴DF=$\frac{1}{2}$FB,
∴$\frac{DF}{AF}=\frac{\frac{1}{2}BF}{AF}=\frac{1}{4}$,
∵CE⊥AD,
∴tan∠ACE=$\frac{AE}{EC}$,
∵∠CAE+∠ACE=90°,∠CAE+∠DAB=90°,
∴∠ACE=∠DAF,
∴tan∠ACE=tan∠DAF=$\frac{AE}{EC}=\frac{DF}{AF}$=$\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 此题主要考查了相似三角形的性质以及平行线分线段成比例定理、锐角三角函数关系等知识,正确得出tan∠ACE=tan∠DAF的值是解题关键.

练习册系列答案
相关题目
 已知△ABC中,∠ABC为钝角.请你按要求作图(不写作法,但要保留作图痕迹):
已知△ABC中,∠ABC为钝角.请你按要求作图(不写作法,但要保留作图痕迹): 如图,在Rt△ABC中,∠C=90°,DE⊥AB垂足为点D,BC=BD,求证:DE=CE.(提示:连接BE)
如图,在Rt△ABC中,∠C=90°,DE⊥AB垂足为点D,BC=BD,求证:DE=CE.(提示:连接BE) (1)若(m-2)2+|n+3|=0,求3m-n2的值.
(1)若(m-2)2+|n+3|=0,求3m-n2的值.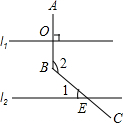 如图,直线l1∥l2,AB⊥l1,垂足为O,BC与l2相交与点E,若∠2=125°,则∠1=35度.
如图,直线l1∥l2,AB⊥l1,垂足为O,BC与l2相交与点E,若∠2=125°,则∠1=35度.
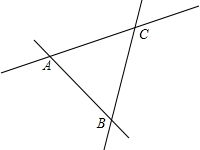 如图所示,三条公路分别相交于A、B、C三点,现计划修建一个加油站,要求该加油站到三条公路的距离相等,用直尺和圆规作出加油站O的位置.(不写作法,请保留作图痕迹)
如图所示,三条公路分别相交于A、B、C三点,现计划修建一个加油站,要求该加油站到三条公路的距离相等,用直尺和圆规作出加油站O的位置.(不写作法,请保留作图痕迹)