题目内容
17.y=$\sqrt{4-{x^2}}$的最大值m与最小值n的和m+n=2.分析 根据二次根是有意义的条件,可得出最大值m=2,最小值n=0,从而得出答案.
解答 解:∵y=$\sqrt{4-{x^2}}$的最大值m=2,最小值n=0,
∴m+n=2,
故答案为2.
点评 本题考查了二次根式有意义的条件,性质:二次根式中的被开方数必须是非负数,否则二次根式无意义.同时考查了非负数的性质,几个非负数的和为0,这几个非负数都为0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8. 如图,在梯形ABCD中,AB∥CD,∠ADC=90度,AB=AD=2,E是AD边上一点(点E不与A,D重合),BE的垂直平分线交边AB于M,交直线CD于N.设四边形ADNM的面积为S,则S的最大值是( )
如图,在梯形ABCD中,AB∥CD,∠ADC=90度,AB=AD=2,E是AD边上一点(点E不与A,D重合),BE的垂直平分线交边AB于M,交直线CD于N.设四边形ADNM的面积为S,则S的最大值是( )
 如图,在梯形ABCD中,AB∥CD,∠ADC=90度,AB=AD=2,E是AD边上一点(点E不与A,D重合),BE的垂直平分线交边AB于M,交直线CD于N.设四边形ADNM的面积为S,则S的最大值是( )
如图,在梯形ABCD中,AB∥CD,∠ADC=90度,AB=AD=2,E是AD边上一点(点E不与A,D重合),BE的垂直平分线交边AB于M,交直线CD于N.设四边形ADNM的面积为S,则S的最大值是( )| A. | $\frac{5}{3}$ | B. | 2 | C. | $\frac{4}{3}$ | D. | $\frac{5}{2}$ |
5. 如图,Rt△ACB中,AC=BC,∠ACB=90°,D、E为AB上两点,且∠DCE=45°,F为△ABC外一点,且FB⊥AB,FC⊥CD,则下列结论:
如图,Rt△ACB中,AC=BC,∠ACB=90°,D、E为AB上两点,且∠DCE=45°,F为△ABC外一点,且FB⊥AB,FC⊥CD,则下列结论:
①CD=CF;②CE垂直但不平分DF;③AD2+BD2=2DC2;④DE2-BE2=AD2.
其中正确的个数是( )
 如图,Rt△ACB中,AC=BC,∠ACB=90°,D、E为AB上两点,且∠DCE=45°,F为△ABC外一点,且FB⊥AB,FC⊥CD,则下列结论:
如图,Rt△ACB中,AC=BC,∠ACB=90°,D、E为AB上两点,且∠DCE=45°,F为△ABC外一点,且FB⊥AB,FC⊥CD,则下列结论:①CD=CF;②CE垂直但不平分DF;③AD2+BD2=2DC2;④DE2-BE2=AD2.
其中正确的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.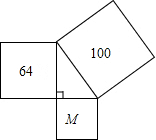 如图,三个正方形围成一个直角三角形,64、100分别为所在正方形的面积,则图中字母所代表的正方形的边长是( )
如图,三个正方形围成一个直角三角形,64、100分别为所在正方形的面积,则图中字母所代表的正方形的边长是( )
 如图,三个正方形围成一个直角三角形,64、100分别为所在正方形的面积,则图中字母所代表的正方形的边长是( )
如图,三个正方形围成一个直角三角形,64、100分别为所在正方形的面积,则图中字母所代表的正方形的边长是( )| A. | 36 | B. | $4\sqrt{41}$ | C. | 6 | D. | 164 |
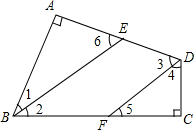 如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,BE∥DF,求证:DF平分∠ADC.
如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,BE∥DF,求证:DF平分∠ADC.
 如图,M、P分别为△ABC的AB、AC上的点,且AM=BM,AP=2CP,BP与CM相交于N,已知PN=1,则PB的长为( )
如图,M、P分别为△ABC的AB、AC上的点,且AM=BM,AP=2CP,BP与CM相交于N,已知PN=1,则PB的长为( )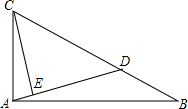 如图,已知点D是Rt△ABC的斜边BC上的一点,tanB=$\frac{1}{2}$,BC=3BD,CE⊥AD,则$\frac{AE}{CE}$=$\frac{1}{4}$.
如图,已知点D是Rt△ABC的斜边BC上的一点,tanB=$\frac{1}{2}$,BC=3BD,CE⊥AD,则$\frac{AE}{CE}$=$\frac{1}{4}$.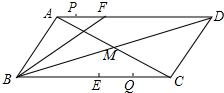 如图,在平行四边形ABCD中,AC与BD交于点M,点F在AD上,AF=6cm,BF=12cm,∠FBM=∠CBM,点E是BC的中点,若点P以1cm/秒的速度从点A出发,沿AD向点F运动;点Q同时以2cm/秒的速度从点C出发,沿CB向点B运动.点P运动到F点时停止运动,点Q也同时停止运动.当点P运动3或5秒时,以点P、Q、E、F为顶点的四边形是平行四边形.
如图,在平行四边形ABCD中,AC与BD交于点M,点F在AD上,AF=6cm,BF=12cm,∠FBM=∠CBM,点E是BC的中点,若点P以1cm/秒的速度从点A出发,沿AD向点F运动;点Q同时以2cm/秒的速度从点C出发,沿CB向点B运动.点P运动到F点时停止运动,点Q也同时停止运动.当点P运动3或5秒时,以点P、Q、E、F为顶点的四边形是平行四边形.