题目内容
14. (1)若(m-2)2+|n+3|=0,求3m-n2的值.
(1)若(m-2)2+|n+3|=0,求3m-n2的值.(2)a、b在数轴上的位置如图所示,化简:|a+b|-2|b-a|=b-3a.
分析 (1)利用非负数的性质求出m与n的值,代入原式计算即可得到结果;
(2)根据数轴上点的位置判断出绝对值里边式子的正负,利用绝对值的代数意义化简,去括号合并即可得到结果.
解答 解:(1)∵(m-2)2+|n+3|=0,
∴m=2,n=-3,
则原式=6-9=-3;
(2)根据数轴上点的位置得:b<0<a,且|a|<|b|,
∴a+b<0,b-a<0,
则原式=-a-b+2b-2a=b-3a,
故答案为:b-3a
点评 此题考查了整式的加减,以及非负数的性质,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
5. 如图,Rt△ACB中,AC=BC,∠ACB=90°,D、E为AB上两点,且∠DCE=45°,F为△ABC外一点,且FB⊥AB,FC⊥CD,则下列结论:
如图,Rt△ACB中,AC=BC,∠ACB=90°,D、E为AB上两点,且∠DCE=45°,F为△ABC外一点,且FB⊥AB,FC⊥CD,则下列结论:
①CD=CF;②CE垂直但不平分DF;③AD2+BD2=2DC2;④DE2-BE2=AD2.
其中正确的个数是( )
 如图,Rt△ACB中,AC=BC,∠ACB=90°,D、E为AB上两点,且∠DCE=45°,F为△ABC外一点,且FB⊥AB,FC⊥CD,则下列结论:
如图,Rt△ACB中,AC=BC,∠ACB=90°,D、E为AB上两点,且∠DCE=45°,F为△ABC外一点,且FB⊥AB,FC⊥CD,则下列结论:①CD=CF;②CE垂直但不平分DF;③AD2+BD2=2DC2;④DE2-BE2=AD2.
其中正确的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19. 如图,在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次将点A向左移动3个单位长度到达点A1,第二次将点A1向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,…按照这种移动规律进行下去,第51次移动到点A51,那么点A51所表示的数为( )
如图,在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次将点A向左移动3个单位长度到达点A1,第二次将点A1向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,…按照这种移动规律进行下去,第51次移动到点A51,那么点A51所表示的数为( )
 如图,在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次将点A向左移动3个单位长度到达点A1,第二次将点A1向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,…按照这种移动规律进行下去,第51次移动到点A51,那么点A51所表示的数为( )
如图,在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次将点A向左移动3个单位长度到达点A1,第二次将点A1向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,…按照这种移动规律进行下去,第51次移动到点A51,那么点A51所表示的数为( )| A. | -74 | B. | -77 | C. | -80 | D. | -83 |
3.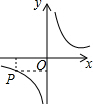 如图,双曲线上任意点P,向x、y轴分别作垂线围成的矩形面积为2,那么反比例函数的解析式是( )
如图,双曲线上任意点P,向x、y轴分别作垂线围成的矩形面积为2,那么反比例函数的解析式是( )
 如图,双曲线上任意点P,向x、y轴分别作垂线围成的矩形面积为2,那么反比例函数的解析式是( )
如图,双曲线上任意点P,向x、y轴分别作垂线围成的矩形面积为2,那么反比例函数的解析式是( )| A. | y=$\frac{1}{x}$ | B. | y=$\frac{2}{x}$ | C. | y=-$\frac{1}{x}$ | D. | y=-$\frac{2}{x}$ |
 如图,M、P分别为△ABC的AB、AC上的点,且AM=BM,AP=2CP,BP与CM相交于N,已知PN=1,则PB的长为( )
如图,M、P分别为△ABC的AB、AC上的点,且AM=BM,AP=2CP,BP与CM相交于N,已知PN=1,则PB的长为( )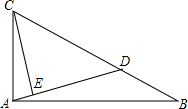 如图,已知点D是Rt△ABC的斜边BC上的一点,tanB=$\frac{1}{2}$,BC=3BD,CE⊥AD,则$\frac{AE}{CE}$=$\frac{1}{4}$.
如图,已知点D是Rt△ABC的斜边BC上的一点,tanB=$\frac{1}{2}$,BC=3BD,CE⊥AD,则$\frac{AE}{CE}$=$\frac{1}{4}$.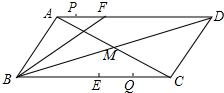 如图,在平行四边形ABCD中,AC与BD交于点M,点F在AD上,AF=6cm,BF=12cm,∠FBM=∠CBM,点E是BC的中点,若点P以1cm/秒的速度从点A出发,沿AD向点F运动;点Q同时以2cm/秒的速度从点C出发,沿CB向点B运动.点P运动到F点时停止运动,点Q也同时停止运动.当点P运动3或5秒时,以点P、Q、E、F为顶点的四边形是平行四边形.
如图,在平行四边形ABCD中,AC与BD交于点M,点F在AD上,AF=6cm,BF=12cm,∠FBM=∠CBM,点E是BC的中点,若点P以1cm/秒的速度从点A出发,沿AD向点F运动;点Q同时以2cm/秒的速度从点C出发,沿CB向点B运动.点P运动到F点时停止运动,点Q也同时停止运动.当点P运动3或5秒时,以点P、Q、E、F为顶点的四边形是平行四边形.