题目内容
14. 已知:如图,CE、CF分别是△ABC的内、外角平分线,过点A作CE、CF的垂线,垂足分别为E、F,且∠ACB=90°,求证:四边形AECF是正方形.
已知:如图,CE、CF分别是△ABC的内、外角平分线,过点A作CE、CF的垂线,垂足分别为E、F,且∠ACB=90°,求证:四边形AECF是正方形.
分析 先证明四边形AECF是矩形,再由∠ACE=∠EAC=45°,证出 AE=CE即可.
解答 证明:∵CE、CF分别是△ABC的内外角平分线,
∴∠ACE+∠ACF=$\frac{1}{2}$×180°=90°,
∵AE⊥CE,AF⊥CF,
∴∠AEC=∠AFC=90°,
∴四边形AECF是矩形,
∵∠ACE=$\frac{1}{2}$∠ACB=45°,
∴∠EAC=45°=∠ACE,
∴AE=CE,
∴四边形AECF是正方形.
点评 本题考查了正方形的判定、矩形的判定、等腰三角形的判定;熟记矩形的判定方法,证出AE=CE是解决问题的关键.

练习册系列答案
相关题目
2.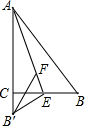 如图,在Rt△ABC,∠ACB=90°,现将Rt△ABC沿AE折叠,使AB边与AC边重合,B点落在B′处,在线段AE上取点F,使点F到AC,BC的距离相等,连接B′F,则∠B′FE的度数为( )
如图,在Rt△ABC,∠ACB=90°,现将Rt△ABC沿AE折叠,使AB边与AC边重合,B点落在B′处,在线段AE上取点F,使点F到AC,BC的距离相等,连接B′F,则∠B′FE的度数为( )
 如图,在Rt△ABC,∠ACB=90°,现将Rt△ABC沿AE折叠,使AB边与AC边重合,B点落在B′处,在线段AE上取点F,使点F到AC,BC的距离相等,连接B′F,则∠B′FE的度数为( )
如图,在Rt△ABC,∠ACB=90°,现将Rt△ABC沿AE折叠,使AB边与AC边重合,B点落在B′处,在线段AE上取点F,使点F到AC,BC的距离相等,连接B′F,则∠B′FE的度数为( )| A. | 30° | B. | 36° | C. | 45° | D. | 60° |
5.两条平行线被第三条直线所截,一对同旁内角的比为2:7,则这两个角中较大的角的度数为( )
| A. | 40° | B. | 70° | C. | 100° | D. | 140° |
2.若a>1,在下面四组数中,能组成直角三角形的是( )
| A. | a-1、a+1、$\sqrt{1+{a}^{2}}$ | B. | 3(a-1)、4(a-1)、5(a-1) | C. | a-1、a、a+1 | D. | a+2、a、$\sqrt{2{a}^{2}+4}$ |
3.下列各组数中,以a、b、c为边的三角形不是直角三角形的是( )
| A. | a=1.5,b=2,c=3 | B. | a=3,b=4,c=5 | C. | a=6,b=8,c=10 | D. | a=7,b=24,c=25 |
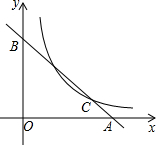 如图,C是函数y=$\frac{8}{x}$(x>0)图象上的一个动点,过点C的直线CD分别交x轴,y轴于点A,B,且满足BC=2CA,求△AOB的面积.
如图,C是函数y=$\frac{8}{x}$(x>0)图象上的一个动点,过点C的直线CD分别交x轴,y轴于点A,B,且满足BC=2CA,求△AOB的面积.