题目内容
9.请你尝试用不同的方法对多项式x3+x2-x-1进行因式分解.分析 利用分组分解法,把其中两项分成一组另外两项分成一组利用提公因式法和平方差公式即可分解.
解答 解:原式=x2(x+1)-(x+1)
=(x+1)(x2-1)
=(x+1)(x+1)(x-1)
=(x+1)2(x-1);
原式=(x3-x)+(x2-1)
=x(x2-1)+(x2-1)
=(x2-1)(x+1)
=(x+1)2(x-1).
点评 本题主要考查了非负数的性质和分组分解法分解因式,用分组分解法进行因式分解的难点是采用两两分组还是三一分组.本题利用的两两分法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.下列计算正确的是( )
| A. | a3+a3=a6 | B. | (2a)3=2a3 | C. | (a3)2=a5 | D. | a•a5=a6 |
17.已知xy=4,x-y=5,则x2+3xy+y2=( )
| A. | 54 | B. | 45 | C. | -54 | D. | -45 |
 【阅读理解】
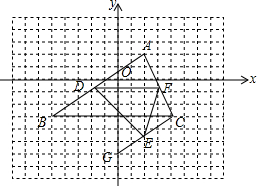
【阅读理解】 已知:如图,CE、CF分别是△ABC的内、外角平分线,过点A作CE、CF的垂线,垂足分别为E、F,且∠ACB=90°,求证:四边形AECF是正方形.
已知:如图,CE、CF分别是△ABC的内、外角平分线,过点A作CE、CF的垂线,垂足分别为E、F,且∠ACB=90°,求证:四边形AECF是正方形.