题目内容
5.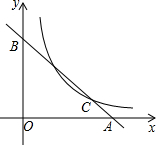 如图,C是函数y=$\frac{8}{x}$(x>0)图象上的一个动点,过点C的直线CD分别交x轴,y轴于点A,B,且满足BC=2CA,求△AOB的面积.
如图,C是函数y=$\frac{8}{x}$(x>0)图象上的一个动点,过点C的直线CD分别交x轴,y轴于点A,B,且满足BC=2CA,求△AOB的面积.
分析 作CE⊥OA于E,CF⊥OB于F,根据平行线分线段成比例定理得出$\frac{CE}{OB}$=$\frac{CA}{AB}$=$\frac{1}{3}$,$\frac{CF}{OA}$=$\frac{BC}{AB}$=$\frac{2}{3}$,设C(a,$\frac{8}{a}$),则CFCF=a,CE=$\frac{8}{a}$,即可求得OB=$\frac{24}{a}$,OA=$\frac{3}{2}$a,根据三角形面积公式即可求得.
解答 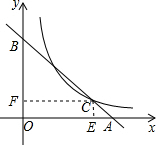 解:作CE⊥OA于E,CF⊥OB于F,
解:作CE⊥OA于E,CF⊥OB于F,
∵CE∥OB,CF∥OA,
∴$\frac{CE}{OB}$=$\frac{CA}{AB}$,$\frac{CF}{OA}$=$\frac{BC}{AB}$,
∵BC=2CA,
∴$\frac{CA}{AB}$=$\frac{1}{3}$,$\frac{BC}{AB}$=$\frac{2}{3}$,
设C(a,$\frac{8}{a}$),则CF=a,CE=$\frac{8}{a}$,
∴$\frac{\frac{8}{a}}{OB}$=$\frac{1}{3}$,$\frac{a}{OA}$=$\frac{2}{3}$
∴OB=$\frac{24}{a}$,OA=$\frac{3}{2}$a,
∴△AOB的面积=$\frac{1}{2}$×OA×OB=$\frac{1}{2}$×$\frac{3a}{2}$×$\frac{24}{a}$=18.
点评 本题考查了反比例函数和一次函数的交点问题,用C的坐标表示OA、OB的值是解题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
17.已知xy=4,x-y=5,则x2+3xy+y2=( )
| A. | 54 | B. | 45 | C. | -54 | D. | -45 |
14.下列计算正确的是( )
| A. | 3$\sqrt{3}-\sqrt{3}$=3 | B. | 2$\sqrt{3}+3\sqrt{3}=5\sqrt{3}$ | C. | $\frac{2\sqrt{3}}{5}+\frac{3\sqrt{2}}{5}=\sqrt{5}$ | D. | 3$\sqrt{6}-6\sqrt{6}=3\sqrt{6}$ |
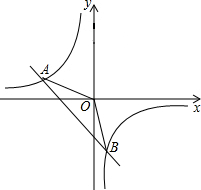 如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=$\frac{m}{x}$(m为常数,且m≠0)的图象交于点A(-2,1)、B(1,-n)
如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=$\frac{m}{x}$(m为常数,且m≠0)的图象交于点A(-2,1)、B(1,-n)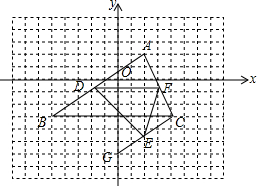 【阅读理解】
【阅读理解】 已知:如图,CE、CF分别是△ABC的内、外角平分线,过点A作CE、CF的垂线,垂足分别为E、F,且∠ACB=90°,求证:四边形AECF是正方形.
已知:如图,CE、CF分别是△ABC的内、外角平分线,过点A作CE、CF的垂线,垂足分别为E、F,且∠ACB=90°,求证:四边形AECF是正方形.