题目内容
2.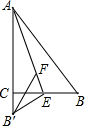 如图,在Rt△ABC,∠ACB=90°,现将Rt△ABC沿AE折叠,使AB边与AC边重合,B点落在B′处,在线段AE上取点F,使点F到AC,BC的距离相等,连接B′F,则∠B′FE的度数为( )
如图,在Rt△ABC,∠ACB=90°,现将Rt△ABC沿AE折叠,使AB边与AC边重合,B点落在B′处,在线段AE上取点F,使点F到AC,BC的距离相等,连接B′F,则∠B′FE的度数为( )| A. | 30° | B. | 36° | C. | 45° | D. | 60° |
分析 根据三角形角平分线的定义可知∠AFB=180°-(∠FAB+∠FBA)=180°-$\frac{1}{2}$(∠BAC+∠CBA)=180°-45°=135°,由此即可解决问题.
解答 解: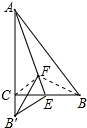 连接BF、B′F,
连接BF、B′F,
∵△AEB′是由△AEB翻折,
∴∠EAB=∠EAB′,∠BFE=∠B′FE,
∵点F到AC,BC的距离相等,
∴CF平分∠ACB,
∴BF平分∠ABC,
∴∠AFB=180°-(∠FAB+∠FBA)=180°-$\frac{1}{2}$(∠BAC+∠CBA)=180°-$\frac{1}{2}$×90°=180°-45°=135°.
∴∠BFE=180°-∠AFB=45°.
故选C.
点评 本题考查翻折变换、三角形内角和定理、角平分线的性质等知识,解题的关键是熟练应用三角形内角和定理解决问题,属于中考常考题型.

练习册系列答案
相关题目
17.已知xy=4,x-y=5,则x2+3xy+y2=( )
| A. | 54 | B. | 45 | C. | -54 | D. | -45 |
10.下列关于x的方程中,无理方程是( )
| A. | ${x^2}+\sqrt{5}x+1=0$ | B. | $\sqrt{2}x+1=0$ | C. | $\sqrt{x+1}+\sqrt{2}=0$ | D. | $\sqrt{a-1}$+2x=7 |
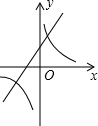
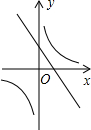

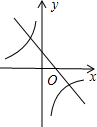
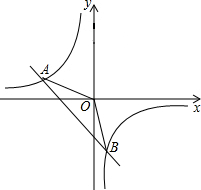 如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=$\frac{m}{x}$(m为常数,且m≠0)的图象交于点A(-2,1)、B(1,-n)
如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=$\frac{m}{x}$(m为常数,且m≠0)的图象交于点A(-2,1)、B(1,-n) 已知:如图,CE、CF分别是△ABC的内、外角平分线,过点A作CE、CF的垂线,垂足分别为E、F,且∠ACB=90°,求证:四边形AECF是正方形.
已知:如图,CE、CF分别是△ABC的内、外角平分线,过点A作CE、CF的垂线,垂足分别为E、F,且∠ACB=90°,求证:四边形AECF是正方形.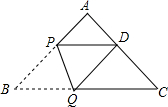 如图,在三角形ABC中,∠A=90°,AB=AC=2,将△ABC折叠,使点B落在边AC上点D (不与点A重合)处,折痕为PQ,当重叠部分△PQD为等腰三角形时,则AD的长为2或2$\sqrt{2}$-2.
如图,在三角形ABC中,∠A=90°,AB=AC=2,将△ABC折叠,使点B落在边AC上点D (不与点A重合)处,折痕为PQ,当重叠部分△PQD为等腰三角形时,则AD的长为2或2$\sqrt{2}$-2.