题目内容
19．已知三角形ABC的周长为16，面积为32，则其内切圆半径为4．分析 利用圆的内切圆的性质，以及三角形的面积公式：三角形的面积=$\frac{1}{2}$×三角形的周长×内切圆的半径，代入计算即可求解．
解答 解：设内切圆的半径是r，则$\frac{1}{2}$×16r=32，
解得：r=4．
故答案为：4．
点评 本题考查了三角形的面积公式以及三角形的内切圆，理解三角形的面积=$\frac{1}{2}$×三角形的周长×内切圆的半径是关键．
练习册系列答案
相关题目
9．
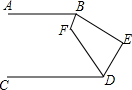如图，AB∥CD，∠ABE和∠CDE的平分线相交于点F，∠F=125°，则∠E的度数为（ ）
如图，AB∥CD，∠ABE和∠CDE的平分线相交于点F，∠F=125°，则∠E的度数为（ ）| A． | 120° | B． | 115° | C． | 110° | D． | 105° |
已知：如图，CE、CF分别是△ABC的内、外角平分线，过点A作CE、CF的垂线，垂足分别为E、F，且∠ACB=90°，求证：四边形AECF是正方形．
10．下列关于x的方程中，无理方程是（ ）
| A． | ${x^2}+\sqrt{5}x+1=0$ | B． | $\sqrt{2}x+1=0$ | C． | $\sqrt{x+1}+\sqrt{2}=0$ | D． | $\sqrt{a-1}$+2x=7 |
