题目内容
2.已知A=(a+b)2+a(3a-2b).(1)化简A;
(2)当a,b满足$\sqrt{2a+1}+|{b-1}|=0$时,求A的值.
分析 (1)先算乘法,再合并同类项即可;
(2)先求出a、b的值,再代入求出即可.
解答 解:(1)A=(a+b)2+a(3a-2b)
=a2+2ab+b2+3a2-2ab
=4a2+b2;
(2)∵$\sqrt{2a+1}+|{b-1}|=0$,
∴2a+1=0,b-1=0,
∴$a=-\frac{1}{2},b=1$,
∴$A=4{a^2}+{b^2}=4×{({-\frac{1}{2}})^2}+{1^2}$=2.
点评 本题考查了整式的混合运算和求值的应用,能正确根据整式的运算法则进行化简是解此题的关键.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
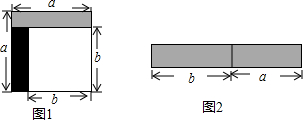 从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).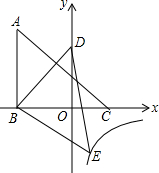 如图,△ABC的三个顶点的坐标分别为A(-3,5),B(-3,0),C(2,0),将△ABC绕点B顺时针旋转一定的角度后得到△DBE,且使点D落在y轴上,与此同时顶点E恰好落在y=$\frac{k}{x}$的图象上,则k的值为( )
如图,△ABC的三个顶点的坐标分别为A(-3,5),B(-3,0),C(2,0),将△ABC绕点B顺时针旋转一定的角度后得到△DBE,且使点D落在y轴上,与此同时顶点E恰好落在y=$\frac{k}{x}$的图象上,则k的值为( )