题目内容
12.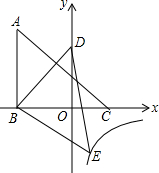 如图,△ABC的三个顶点的坐标分别为A(-3,5),B(-3,0),C(2,0),将△ABC绕点B顺时针旋转一定的角度后得到△DBE,且使点D落在y轴上,与此同时顶点E恰好落在y=$\frac{k}{x}$的图象上,则k的值为( )
如图,△ABC的三个顶点的坐标分别为A(-3,5),B(-3,0),C(2,0),将△ABC绕点B顺时针旋转一定的角度后得到△DBE,且使点D落在y轴上,与此同时顶点E恰好落在y=$\frac{k}{x}$的图象上,则k的值为( )| A. | -3 | B. | -4 | C. | -5 | D. | -3$\sqrt{2}$ |
分析 利用点A、B、C的坐标得到AB⊥x轴,AB=5,BC=5,AC=5$\sqrt{2}$,再根据旋转的性质得BD=AB=5,BE=BC=5,DE=AC=5$\sqrt{2}$,接着确定D点坐标,设E(a,b),利用两点间的距离公式得到(a+3)2+b2=25①,a2+(b-4)2=50②,然后解方程组求出a和b得到E点坐标,最后利用反比例函数图象上点的坐标特征求k的值.
解答 解:∵A(-3,5),B(-3,0),C(2,0),
∴AB⊥x轴,AB=5,BC=5,
∴AC=5$\sqrt{2}$,
∵△ABC绕点B顺时针旋转一定的角度后得到△DBE,且使点D落在y轴上,
∴BD=AB=5,BE=BC=5,DE=AC=5$\sqrt{2}$,
在Rt△OBD中,OD=$\sqrt{B{D}^{2}-O{B}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴D(0,4),
设E(a,b),
∴BE2=(a+3)2+b2=25①,DE2=a2+(b-4)2=50②,
①-②得b=$\frac{-3a-9}{4}$③,
把③代入①整理得a2+6a-7=0,解得a1=-7(舍去),a2=1,
当a=1时,b=-3,
∴E(1,-3),
把E(1,-3)代入y=$\frac{k}{x}$得k=1×(-3)=-3.
故选A.
点评 本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.解决本题的关键是利用两点间的距离公式建立方程组.

练习册系列答案
相关题目
3.某商家经销一种绿茶,用于装修门面已投资3000元.已知绿茶每千克成本50元,经研究发现销量y(kg)随销售单价x(元/kg)的变化而变化,具体变化规律如表所示:
设该绿茶的月销售利润为w(元)(销售利润=单价×销售量-成本)
(1)请根据上表,写出y与x之间的函数关系式(不必写出自变量x的取值范围);
(2)求w与x之间的函数关系式(不必写出自变量x的取值范围),并求出x为何值时,w的值最大?
(3)若在第一个月里,按使w获得最大值的销售单价进行销售后,在第二个月里受物价部门干预,销售单价不得高于80元,要想在全部收回装修投资的基础上使第二个月的利润至少达到1700元,那么第二个月时里应该确定销售单价在什么范围内?
| 销售单价x(元/kg) | … | 70 | 75 | 80 | 85 | 90 | … |
| 月销售量y(kg) | … | 100 | 90 | 80 | 70 | 60 | … |
(1)请根据上表,写出y与x之间的函数关系式(不必写出自变量x的取值范围);
(2)求w与x之间的函数关系式(不必写出自变量x的取值范围),并求出x为何值时,w的值最大?
(3)若在第一个月里,按使w获得最大值的销售单价进行销售后,在第二个月里受物价部门干预,销售单价不得高于80元,要想在全部收回装修投资的基础上使第二个月的利润至少达到1700元,那么第二个月时里应该确定销售单价在什么范围内?
20.某课外小组的同学们在社会实践活动中调查了20户家庭某月的用电量,如表所示:
则这20户家庭该月用电量的众数和中位数分别是( )
| 用电量(度) | 120 | 140 | 160 | 180 | 200 |
| 户数 | 2 | 3 | 6 | 7 | 2 |
| A. | 180,180 | B. | 160,180 | C. | 160,160 | D. | 180,160 |
4.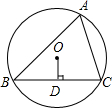 如图,△ABC内接于⊙O,作OD⊥BC于点D,若∠A=60°,则OD:CD的值为( )
如图,△ABC内接于⊙O,作OD⊥BC于点D,若∠A=60°,则OD:CD的值为( )
 如图,△ABC内接于⊙O,作OD⊥BC于点D,若∠A=60°,则OD:CD的值为( )
如图,△ABC内接于⊙O,作OD⊥BC于点D,若∠A=60°,则OD:CD的值为( )| A. | 1:2 | B. | 1:$\sqrt{2}$ | C. | 1:$\sqrt{3}$ | D. | 2:$\sqrt{3}$ |
 如图,在△ABC中,DE∥BC,分别交AB,AC于点D,E.若AD=4,DB=3,BC=9,则DE的长为$\frac{36}{7}$.
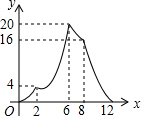
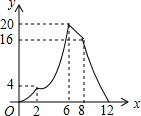
如图,在△ABC中,DE∥BC,分别交AB,AC于点D,E.若AD=4,DB=3,BC=9,则DE的长为$\frac{36}{7}$.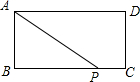 如图,在矩形ABCD中,AB=2,AD=4,矩形边上一动点P沿A→B→C→D→A的路径移动.设点P经过的路径长为x,AP2=y,则下列能大致反映y与x的函数关系的图象是( )
如图,在矩形ABCD中,AB=2,AD=4,矩形边上一动点P沿A→B→C→D→A的路径移动.设点P经过的路径长为x,AP2=y,则下列能大致反映y与x的函数关系的图象是( )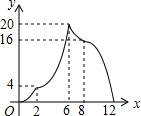

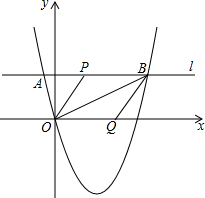 如图,抛物线y=ax2+3(a-1)x(a>0)经过点A(-3,m),过点A作直线l平行于x轴与抛物线交于另一点B,在x轴上取点Q,连接BQ,使得∠QBO=∠ABO,过点O作OP平行BQ交l于点P,若AP=$\frac{1}{2}$AB,则a的值为$\frac{1}{9}$.
如图,抛物线y=ax2+3(a-1)x(a>0)经过点A(-3,m),过点A作直线l平行于x轴与抛物线交于另一点B,在x轴上取点Q,连接BQ,使得∠QBO=∠ABO,过点O作OP平行BQ交l于点P,若AP=$\frac{1}{2}$AB,则a的值为$\frac{1}{9}$.