题目内容
10.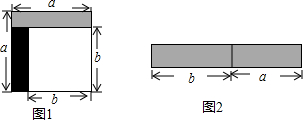 从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).(1)上述操作能验证的等式是B;(请选择正确的一个)
A、a2-2ab+b2=(a-b)2
B、a2-b2=(a+b)(a-b)
C、a2+ab=a(a+b)
(2)应用你从(1)选出的等式,完成下列各题:
①已知x2-4y2=12,x+2y=4,求x-2y的值.
②计算:(1-$\frac{1}{{2}^{2}}$)(1-$\frac{1}{{3}^{2}}$)(1-$\frac{1}{{4}^{2}}$)…(1-$\frac{1}{4{9}^{2}}$)(1-$\frac{1}{5{0}^{2}}$).
分析 (1)观察图1与图2,根据两图形阴影部分面积相等验证平方差公式即可;
(2)①已知第一个等式左边利用平方差公式化简,将第二个等式代入求出所求式子的值即可;②原式利用平方差公式变形,约分即可得到结果.
解答 解:(1)根据图形得:a2-b2=(a+b)(a-b),
上述操作能验证的等式是B,
故答案为:B;
(2)①∵x2-4y2=(x+2y)(x-2y)=12,x+2y=4,
∴x-2y=3;
②原式=(1-$\frac{1}{2}$)(1+$\frac{1}{2}$)(1-$\frac{1}{3}$)(1+$\frac{1}{3}$)…(1-$\frac{1}{49}$)(1+$\frac{1}{49}$)(1-$\frac{1}{50}$)(1+$\frac{1}{50}$)=$\frac{1}{2}$×$\frac{3}{2}$×$\frac{2}{3}$×$\frac{4}{3}$×$\frac{3}{4}$×$\frac{5}{4}$×…×$\frac{48}{49}$×$\frac{50}{49}$×$\frac{49}{50}$×$\frac{51}{50}$=$\frac{1}{2}$×$\frac{51}{50}$=$\frac{51}{100}$.
点评 此题考查了平方差公式的几何背景,熟练掌握平方差公式是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.如果(x+q)(x+5)=px2+7x+10,则q与p的值分别是( )
| A. | 5、2 | B. | 1、5 | C. | 2、1 | D. | 2、5 |
19.已知a-2b+3=0,则代数式5+2b-a的值是( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
20.某课外小组的同学们在社会实践活动中调查了20户家庭某月的用电量,如表所示:
则这20户家庭该月用电量的众数和中位数分别是( )
| 用电量(度) | 120 | 140 | 160 | 180 | 200 |
| 户数 | 2 | 3 | 6 | 7 | 2 |
| A. | 180,180 | B. | 160,180 | C. | 160,160 | D. | 180,160 |
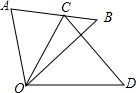 如图,△COD是由△AOB绕点O按顺时针方向旋转40°后得到的图形,点C恰好在边AB上.若∠AOD=100°,则∠D的度数是50°.
如图,△COD是由△AOB绕点O按顺时针方向旋转40°后得到的图形,点C恰好在边AB上.若∠AOD=100°,则∠D的度数是50°.