题目内容
14.先化简,再求值:(a+b)(a-b)+b(b-2),其中a=2,b=1.5.分析 先算乘法,再算加减,把a=2,b=1.5代入进行计算即可.
解答 解:原式=a2-b2+b2-2b
=a2-2b.
当a=2,b=1.5时,原式=4-2×1.5=4-3=1.
点评 本题考查的是整式的混合运算-化简求值,在有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.

练习册系列答案
相关题目
19.已知a-2b+3=0,则代数式5+2b-a的值是( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
3.某商家经销一种绿茶,用于装修门面已投资3000元.已知绿茶每千克成本50元,经研究发现销量y(kg)随销售单价x(元/kg)的变化而变化,具体变化规律如表所示:
设该绿茶的月销售利润为w(元)(销售利润=单价×销售量-成本)
(1)请根据上表,写出y与x之间的函数关系式(不必写出自变量x的取值范围);
(2)求w与x之间的函数关系式(不必写出自变量x的取值范围),并求出x为何值时,w的值最大?
(3)若在第一个月里,按使w获得最大值的销售单价进行销售后,在第二个月里受物价部门干预,销售单价不得高于80元,要想在全部收回装修投资的基础上使第二个月的利润至少达到1700元,那么第二个月时里应该确定销售单价在什么范围内?
| 销售单价x(元/kg) | … | 70 | 75 | 80 | 85 | 90 | … |
| 月销售量y(kg) | … | 100 | 90 | 80 | 70 | 60 | … |
(1)请根据上表,写出y与x之间的函数关系式(不必写出自变量x的取值范围);
(2)求w与x之间的函数关系式(不必写出自变量x的取值范围),并求出x为何值时,w的值最大?
(3)若在第一个月里,按使w获得最大值的销售单价进行销售后,在第二个月里受物价部门干预,销售单价不得高于80元,要想在全部收回装修投资的基础上使第二个月的利润至少达到1700元,那么第二个月时里应该确定销售单价在什么范围内?
4.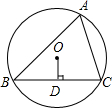 如图,△ABC内接于⊙O,作OD⊥BC于点D,若∠A=60°,则OD:CD的值为( )
如图,△ABC内接于⊙O,作OD⊥BC于点D,若∠A=60°,则OD:CD的值为( )
 如图,△ABC内接于⊙O,作OD⊥BC于点D,若∠A=60°,则OD:CD的值为( )
如图,△ABC内接于⊙O,作OD⊥BC于点D,若∠A=60°,则OD:CD的值为( )| A. | 1:2 | B. | 1:$\sqrt{2}$ | C. | 1:$\sqrt{3}$ | D. | 2:$\sqrt{3}$ |
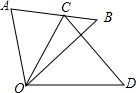 如图,△COD是由△AOB绕点O按顺时针方向旋转40°后得到的图形,点C恰好在边AB上.若∠AOD=100°,则∠D的度数是50°.
如图,△COD是由△AOB绕点O按顺时针方向旋转40°后得到的图形,点C恰好在边AB上.若∠AOD=100°,则∠D的度数是50°.