题目内容
已知点A(1,5),B(3,1),点M在x轴上,当AM-BM最大时,点M的坐标为 .
考点:轴对称-最短路线问题,坐标与图形性质
专题:
分析:连接AB并延长与x轴的交点M,即为所求的点.求出直线AB的解析式,求出直线AB和x轴的交点坐标即可.
解答: 解:设直线AB的解析式是y=kx+b,
解:设直线AB的解析式是y=kx+b,
把A(1,5),B(3,1)代入得:
,
解得:k=-2,b=7,
即直线AB的解析式是y=-2x+7,
把y=0代入得:-2x+7=0,
x=
,
即M的坐标是(
,0),
故答案为(
,0).
 解:设直线AB的解析式是y=kx+b,
解:设直线AB的解析式是y=kx+b,把A(1,5),B(3,1)代入得:
|
解得:k=-2,b=7,
即直线AB的解析式是y=-2x+7,
把y=0代入得:-2x+7=0,
x=
| 7 |
| 2 |
即M的坐标是(
| 7 |
| 2 |
故答案为(
| 7 |
| 2 |
点评:本题考查了轴对称,用待定系数法求一次函数的解析式等知识点的应用,关键是找出M的位置.

练习册系列答案
相关题目
 如图,AB∥DE,∠A=120°,C=80°,则∠D的度数为( )
如图,AB∥DE,∠A=120°,C=80°,则∠D的度数为( )| A、130° | B、120° |
| C、160° | D、145° |
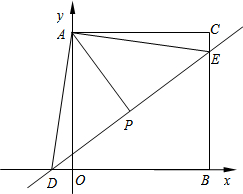 如图,平面直角坐标系中,过点C(28,28)分别作x轴、y轴的垂线,垂足分别为B、A,一次函数y=
如图,平面直角坐标系中,过点C(28,28)分别作x轴、y轴的垂线,垂足分别为B、A,一次函数y=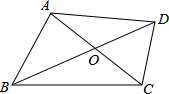 如图,四边形ABCD的对角线AC、BD交于点O,且BD平分AC.若BD=10,AC=6,∠BOC=120°,则四边形ABCD的面积为
如图,四边形ABCD的对角线AC、BD交于点O,且BD平分AC.若BD=10,AC=6,∠BOC=120°,则四边形ABCD的面积为 ”图案.
”图案.