题目内容
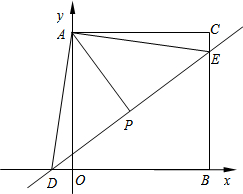 如图,平面直角坐标系中,过点C(28,28)分别作x轴、y轴的垂线,垂足分别为B、A,一次函数y=
如图,平面直角坐标系中,过点C(28,28)分别作x轴、y轴的垂线,垂足分别为B、A,一次函数y=| 3 |
| 4 |
(1)求证:△ADO≌△AEC;
(2)求AP的长.
考点:一次函数综合题
专题:
分析:(1)根据题意即可求得D(-4,0),E(28,24),从而求得OD=CE,然后根据SAS即可求得结论.
(2)根据三角形全等的性质求得∠EAC=∠DAO,进而求得∠DAE=90°.根据直角三角形斜边中线的性质求得AP=
DE.根据勾股定理求得DE=40,即可求得AP的长.
(2)根据三角形全等的性质求得∠EAC=∠DAO,进而求得∠DAE=90°.根据直角三角形斜边中线的性质求得AP=
| 1 |
| 2 |
解答:(1)证明:把y=0,代入y=
x+3得,0=
x+3,解得x=-4,
∴D(-4,0),
把x=28代入y=
x+3得,y=24,
∴E(28,24),
∵C(28,28),
∴CE=28-24=4,
∵OD=4,
∴OD=CE,
在△ADO与△AEC中
∴△ADO≌△AEC(SAS).
(2)解:∵△ADO≌△AEC,
∴∠EAC=∠DAO,
∴∠EAC+∠OAE=∠DAO+∠OAE=90°,
∴∠DAE=90°.
∵P为DE中点,
∴AP=
DE.
在Rt△DBE中,DE2=BD2+BE2=242+322=1600,
∴DE=40,
∴AP=20.
| 3 |
| 4 |
| 3 |
| 4 |
∴D(-4,0),
把x=28代入y=
| 3 |
| 4 |
∴E(28,24),
∵C(28,28),
∴CE=28-24=4,
∵OD=4,
∴OD=CE,
在△ADO与△AEC中
|
∴△ADO≌△AEC(SAS).
(2)解:∵△ADO≌△AEC,
∴∠EAC=∠DAO,
∴∠EAC+∠OAE=∠DAO+∠OAE=90°,
∴∠DAE=90°.
∵P为DE中点,
∴AP=
| 1 |
| 2 |
在Rt△DBE中,DE2=BD2+BE2=242+322=1600,
∴DE=40,
∴AP=20.
点评:本题是一次函数的综合题,考查了一次函数图象上点的坐标特征,三角形全等的判定和性质以及勾股定理的应用,直角三角形中线的性质等,熟练掌握性质定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2015年1月18日,重庆遭遇雾霾天,整个城市被“深埋”,空气中的PM2.5的浓度持续增高.其中PM2.5是指直径小于或等于0.0000025m的颗粒物,将0.0000025m用科学记数法表示是 m.
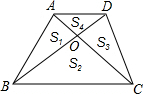 如图,已知在梯形ABCD中,AD∥BC,BC=2AD,如果对角线AC与BD相交于点O,△AOB、△BOC、△COD、△DOA的面积分别记作S1、S2、S3、S4,那么下列结论中,不正确的是( )
如图,已知在梯形ABCD中,AD∥BC,BC=2AD,如果对角线AC与BD相交于点O,△AOB、△BOC、△COD、△DOA的面积分别记作S1、S2、S3、S4,那么下列结论中,不正确的是( )| A、S1=S3 |
| B、S2=2S4 |
| C、S2=2S1 |
| D、S1•S3=S2•S4 |
 如图,在△ABC中,AB=AC,E是BC上一点,D是AC上一点,且AE=AD,若∠DEC=20°,求∠BAE的度数.
如图,在△ABC中,AB=AC,E是BC上一点,D是AC上一点,且AE=AD,若∠DEC=20°,求∠BAE的度数.
 作出如图立体图形的三视图.
作出如图立体图形的三视图.