题目内容
边心距为4
的正六边形的半径为 ,中心角等于 度,面积为 .
| 3 |
考点:正多边形和圆
专题:
分析:根据题意画出图形,先求出∠AOB的度数,再根据直角三角形的性质求出OA的长,再根据S六边形=6S△AOB即可得出结论.
解答: 解:如图所示,
解:如图所示,
∵图中是正六边形,
∴∠AOB=
=60°.
∵OA=OB,
∴△OAB是等边三角形.
∵OD⊥AB,OD=4
,
∴OA=
=
=8.
∴S△AOB=
AB×OD=
×8×4
=16
S六边形=6S△AOB=6×16
=96
.
故答案为:8,60,96
.
 解:如图所示,
解:如图所示,∵图中是正六边形,
∴∠AOB=
| 360° |
| 6 |
∵OA=OB,
∴△OAB是等边三角形.
∵OD⊥AB,OD=4
| 3 |
∴OA=
| OD |
| sin60° |
4
| ||||
|
∴S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
S六边形=6S△AOB=6×16
| 3 |
| 3 |
故答案为:8,60,96
| 3 |
点评:本题考查的是正多边形和圆,熟知正六边形的性质是解答此题的关键.

练习册系列答案
相关题目
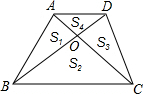 如图,已知在梯形ABCD中,AD∥BC,BC=2AD,如果对角线AC与BD相交于点O,△AOB、△BOC、△COD、△DOA的面积分别记作S1、S2、S3、S4,那么下列结论中,不正确的是( )
如图,已知在梯形ABCD中,AD∥BC,BC=2AD,如果对角线AC与BD相交于点O,△AOB、△BOC、△COD、△DOA的面积分别记作S1、S2、S3、S4,那么下列结论中,不正确的是( )| A、S1=S3 |
| B、S2=2S4 |
| C、S2=2S1 |
| D、S1•S3=S2•S4 |
若a是有理数,则计算正确的是( )
| A、3a-a=3 |
| B、a-(-a)=0 |
| C、a+(-a)=2a |
| D、-a-a=-2a |
 如图,在△ABC中,AB=AC,E是BC上一点,D是AC上一点,且AE=AD,若∠DEC=20°,求∠BAE的度数.
如图,在△ABC中,AB=AC,E是BC上一点,D是AC上一点,且AE=AD,若∠DEC=20°,求∠BAE的度数. 如图所示,居民楼A与马路a相距60m,在距离汽车100m处就可受到噪音影响,试求在路上以9km/h速度行驶的汽车,给A楼的居民带来多长时间的噪音.
如图所示,居民楼A与马路a相距60m,在距离汽车100m处就可受到噪音影响,试求在路上以9km/h速度行驶的汽车,给A楼的居民带来多长时间的噪音.