题目内容
在△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长为 .
考点:勾股定理
专题:分类讨论
分析:本题应分两种情况进行讨论:
(1)当△ABC为锐角三角形时,在Rt△ABD和Rt△ACD中,运用勾股定理可将BD和CD的长求出,两者相加即为BC的长,从而可将△ABC的周长求出;
(2)当△ABC为钝角三角形时,在Rt△ABD和Rt△ACD中,运用勾股定理可将BD和CD的长求出,两者相减即为BC的长,从而可将△ABC的周长求出.
(1)当△ABC为锐角三角形时,在Rt△ABD和Rt△ACD中,运用勾股定理可将BD和CD的长求出,两者相加即为BC的长,从而可将△ABC的周长求出;
(2)当△ABC为钝角三角形时,在Rt△ABD和Rt△ACD中,运用勾股定理可将BD和CD的长求出,两者相减即为BC的长,从而可将△ABC的周长求出.
解答:解:解:此题应分两种情况说明:
(1)当△ABC为锐角三角形时,在Rt△ABD中,
BD=
=
=9,
在Rt△ACD中,
CD=
=
=5
∴BC=5+9=14
∴△ABC的周长为:15+13+14=42;
(2)当△ABC为钝角三角形时,
在Rt△ABD中,BD=
=
=9,
在Rt△ACD中,CD=
=
=5,
∴BC=9-5=4.
∴△ABC的周长为:15+13+4=32
故答案是:42或32.

(1)当△ABC为锐角三角形时,在Rt△ABD中,
BD=
| AB2-AD2 |
| 152-122 |
在Rt△ACD中,
CD=
| AC2-AD2 |
| 132-122 |
∴BC=5+9=14
∴△ABC的周长为:15+13+14=42;
(2)当△ABC为钝角三角形时,
在Rt△ABD中,BD=
| AB2-AD2 |
| 152-122 |
在Rt△ACD中,CD=
| AC2-AD2 |
| 132-122 |
∴BC=9-5=4.
∴△ABC的周长为:15+13+4=32
故答案是:42或32.
点评:此题考查了勾股定理及解直角三角形的知识,在解本题时应分两种情况进行讨论,易错点在于漏解,同学们思考问题一定要全面,有一定难度.

练习册系列答案
相关题目
正多边形的中心角是36°,那么这个正多边形的边数是( )
| A、10 | B、8 | C、6 | D、5 |
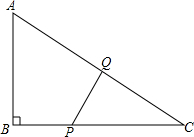 如图,在△ABC中,∠B=90°,AB=6厘米,BC=8厘米,点P从点B出发,沿BC以1厘米/秒的速度向点C移动,点Q从点C出发,沿折线CAB以2厘米/秒的速度向点B移动.问:
如图,在△ABC中,∠B=90°,AB=6厘米,BC=8厘米,点P从点B出发,沿BC以1厘米/秒的速度向点C移动,点Q从点C出发,沿折线CAB以2厘米/秒的速度向点B移动.问: