题目内容
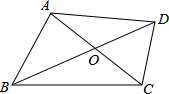 如图,四边形ABCD的对角线AC、BD交于点O,且BD平分AC.若BD=10,AC=6,∠BOC=120°,则四边形ABCD的面积为
如图,四边形ABCD的对角线AC、BD交于点O,且BD平分AC.若BD=10,AC=6,∠BOC=120°,则四边形ABCD的面积为考点:相似三角形的判定与性质,勾股定理
专题:
分析:过点A作AE⊥BD于点E,过点C作CF⊥BD于点F.则通过解直角△AEO和直角△CFO求得AE=CF,所以易求四边形ABCD的面积.
解答: 解:作AE⊥BD,CF⊥BD分别于点E和F.
解:作AE⊥BD,CF⊥BD分别于点E和F.
∵△AOE和△COF中,
,
∴△AOE≌△COF,
∴AE=CF.
在直角△AOE中,∠BOC=120°,则∠AOE=60°,
则CF=AE=OAsin60°=
AC×
=
.
则S四边形ABCD=
BD•AE+
BD•CF=
×10×
+
×10×
=15
.
故答案是:15
.
 解:作AE⊥BD,CF⊥BD分别于点E和F.
解:作AE⊥BD,CF⊥BD分别于点E和F.∵△AOE和△COF中,
|
∴△AOE≌△COF,
∴AE=CF.
在直角△AOE中,∠BOC=120°,则∠AOE=60°,
则CF=AE=OAsin60°=
| 1 |
| 2 |
| ||
| 2 |
3
| ||
| 2 |
则S四边形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
3
| ||
| 2 |
| 1 |
| 2 |
3
| ||
| 2 |
| 3 |
故答案是:15
| 3 |
点评:本题考查了解直角三角形,三角形的面积的计算.求图中相关线段的长度时,也可以根据勾股定理进行解答.

练习册系列答案
相关题目
在下列代数式:
,
,a2b+b+1,
+1中,多项式有( )
| a+b |
| 2 |
| 1 |
| 2 |
| 3 |
| x |
| A、0个 | B、1个 | C、2个 | D、3个 |
正多边形的中心角是36°,那么这个正多边形的边数是( )
| A、10 | B、8 | C、6 | D、5 |
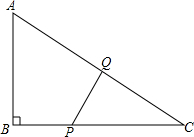 如图,在△ABC中,∠B=90°,AB=6厘米,BC=8厘米,点P从点B出发,沿BC以1厘米/秒的速度向点C移动,点Q从点C出发,沿折线CAB以2厘米/秒的速度向点B移动.问:
如图,在△ABC中,∠B=90°,AB=6厘米,BC=8厘米,点P从点B出发,沿BC以1厘米/秒的速度向点C移动,点Q从点C出发,沿折线CAB以2厘米/秒的速度向点B移动.问: 如图,小方格都是边长为1的正方形,则以格点为圆心,半径为1和2的两种弧围成的“叶片状”阴影图案的面积为
如图,小方格都是边长为1的正方形,则以格点为圆心,半径为1和2的两种弧围成的“叶片状”阴影图案的面积为