题目内容
6．若0°＜α＜90°，那么，以sinα、cosα、tanα•cotα为三边的△ABC的内切圆半径与外接圆半径之和是（ ）| A． | 2sinα•cosα | B． | $\frac{tanα+cotα}{2}$ | C． | $\frac{sinα+cosα}{2}$ | D． | $\frac{1}{sinα•cosα}$ |
分析 先根据三角形的三边关系判断出△ABC的形状，再根据切线长定理即可求出其内切圆的半径，由圆周角定理即可求出外接圆的半径．
解答 解：∵tanα•cotα=1=sinα2+cosα2，
∴△ABC是直角三角形，
如图所示：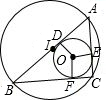
∵AD=AE，CE=CF，BD=BF，
∴内切圆的半径r=$\frac{sinα+cosα-1}{2}$，
∵∠ACB=90°，
∴△ABC外接圆的半径R=$\frac{tanα•cotα}{2}$=$\frac{1}{2}$，
∴r+R=$\frac{sinα+cosα-1}{2}$+$\frac{1}{2}$=$\frac{sinα+cosα}{2}$．
故选C．
点评 本题考查的是三角形的外接圆与内切圆、同角三角函数的关系，根据题意判断出△ABC的形状是解答此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
16．⊙O的内接正三角形与正六边形的面积之比为（ ）
| A． | $\sqrt{2}$：1 | B． | 1：$\sqrt{3}$ | C． | 1：2 | D． | 1：$\sqrt{2}$ |
17．一个自然数a的算术平方根为x，那么a+1的立方根是（ ）
| A． | ±$\root{3}{a+1}$ | B． | $\root{3}{{{{（x+1）}^2}}}$ | C． | $\root{3}{{{x^2}+1}}$ | D． | ±$\root{3}{{{x^2}+1}}$ |
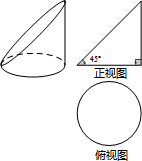某圆柱被一平面所截得到的几何体如图所示，若该几何体的正视图是等腰直角三角形，俯视图是圆（如右图），则它的侧视图是（ ）
