题目内容
14.一枚质地均匀的正六面体骰子,六个面分别标有1、2、3、4、5、6,连续投掷两次.(1)用列表法或画树状图法表示出朝上的面上的数字所有可能出现的结果;
(2)记两次朝上的面上的数字分别为m、n,若把m、n分别作为点P的横坐标和纵坐标,求点P(m,n)在双曲线y=$\frac{12}{x}$上的概率.
分析 (1)利用树状图展示所有36种等可能的结果数;
(2)根据反比例函数图象上点的坐标特征,可判点(2,6),(3,4),(4,3),(6,2)在双曲线y=$\frac{12}{x}$上,于是可根据概率公式计算出点P(m,n)在双曲线y=$\frac{12}{x}$上的概率.
解答 解:(1)画树状图为: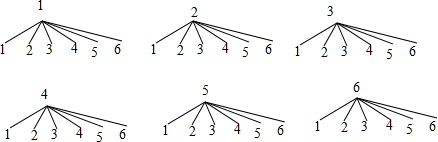
共有36种等可能的结果数;
(2)点P(m,n)在双曲线y=$\frac{12}{x}$上的结果数为4,它们是(2,6),(3,4),(4,3),(6,2),
所以点P(m,n)在双曲线y=$\frac{12}{x}$上的概率=$\frac{4}{36}$=$\frac{1}{9}$.
点评 本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.也考查了反比例函数图象上点的坐标特征.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
5.-64的立方根与$\sqrt{81}$的平方根之和是( )
| A. | -7 | B. | -1或-7 | C. | -13或5 | D. | 5 |
19.小明、小联、小豪人一起玩“剪刀、石头、布”的游戏.每一局三人同时出“剪刀、石头、布”中的一种手势.则小明只赢一人的概率为( )
| A. | $\frac{2}{9}$ | B. | $\frac{4}{9}$ | C. | $\frac{2}{27}$ | D. | $\frac{4}{27}$ |
6.若0°<α<90°,那么,以sinα、cosα、tanα•cotα为三边的△ABC的内切圆半径与外接圆半径之和是( )
| A. | 2sinα•cosα | B. | $\frac{tanα+cotα}{2}$ | C. | $\frac{sinα+cosα}{2}$ | D. | $\frac{1}{sinα•cosα}$ |
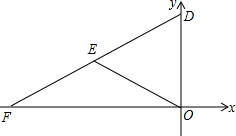 如图,平面直角坐标系中,O为坐标原点,已知直线y=$\frac{1}{2}$x+5分别与x,y轴相交于点F、D,点E在线段DF上,连接OE,且OE=DE.求OE所在的直线解析式.
如图,平面直角坐标系中,O为坐标原点,已知直线y=$\frac{1}{2}$x+5分别与x,y轴相交于点F、D,点E在线段DF上,连接OE,且OE=DE.求OE所在的直线解析式.