题目内容
16．四边形ABCD中，AB∥CD，且AB=CD，则四边形ABCD是平行四边形，理由是一组对边平行且相等的四边形是平行四边形．分析 根据平行四边形的判定定理：一组对边平行且相等的四边形是平行四边形；即可得出结论．
解答 解：四边形ABCD是平行四边形；
理由是：一组对边平行且相等的四边形是平行四边形；
∵AB∥CD，AB=CD，
∴四边形ABCD是平行四边形；
故答案为：平行四边形；一组对边平行且相等的四边形是平行四边形．
点评 本题考查了平行四边形的判定方法；熟练掌握平行四边形的判定方法，并能进行推理论证是解决问题的关键．
练习册系列答案
相关题目
6．若0°＜α＜90°，那么，以sinα、cosα、tanα•cotα为三边的△ABC的内切圆半径与外接圆半径之和是（ ）
| A． | 2sinα•cosα | B． | $\frac{tanα+cotα}{2}$ | C． | $\frac{sinα+cosα}{2}$ | D． | $\frac{1}{sinα•cosα}$ |
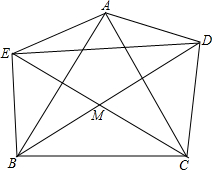如图，△ABC中，D，E是△ABC外两点，M是△ABC内一点．若AE=BE，AD=DC，∠DEM=$\frac{1}{2}$∠AEB，∠EDM=$\frac{1}{2}$∠ADC．求证：MB=MC．
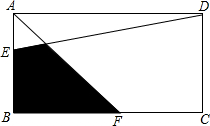面积为1的长方形ABCD中，点E为AB的三等分点，点F为BC中点，求阴影部分的面积．