题目内容
18.设方程x2+(m+6)x+(m-3)=0有两个不同的奇数根,求整数m的值.分析 根据根与系数的关系,得出两根之和和两根之积,进一步利用因式分解探讨得出m的数值即可.
解答 解:设方程x2+(m+6)x+(m-3)=0有两个不同的奇数根为x1、x2,
x1+x2=-(m+6),
x1x2=m-3,
则x1x2+x1+x2=-12,
(x2+1)x1+(x2+1)=-11,
(x1+1)(x2+1)=-11=-1×11,或-11×1,
不妨设x1>x2,
解:判别式=(m+6)2-4(m-3)
=m2+12m+36-4m+12>0
=m2+8m+48>0,
m为一切实数,
方程x2+(m+6)x+(m-3)=0有两个不同的奇数根,
x1+x2=-(m+6)是偶数,
x1x2=m-3是奇数,
由上式得出,m只要是偶数就行了.
即:m=2n.
点评 此题主要考查了一元二次方程的解的情况,通过根与系数的关系以及根的判别式,把求未知系数的范围的问题转化为解不等式组的问题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
6.若0°<α<90°,那么,以sinα、cosα、tanα•cotα为三边的△ABC的内切圆半径与外接圆半径之和是( )
| A. | 2sinα•cosα | B. | $\frac{tanα+cotα}{2}$ | C. | $\frac{sinα+cosα}{2}$ | D. | $\frac{1}{sinα•cosα}$ |
13.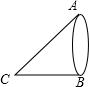 如图,湖的两端有A,B两点,从与BA方向成直角的BC方向上的C点测得CA=130米,CB=120米,则AB为( )
如图,湖的两端有A,B两点,从与BA方向成直角的BC方向上的C点测得CA=130米,CB=120米,则AB为( )
 如图,湖的两端有A,B两点,从与BA方向成直角的BC方向上的C点测得CA=130米,CB=120米,则AB为( )
如图,湖的两端有A,B两点,从与BA方向成直角的BC方向上的C点测得CA=130米,CB=120米,则AB为( )| A. | 30米 | B. | 40米 | C. | 50米 | D. | 60米 |
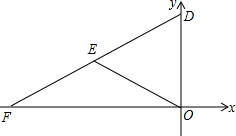 如图,平面直角坐标系中,O为坐标原点,已知直线y=$\frac{1}{2}$x+5分别与x,y轴相交于点F、D,点E在线段DF上,连接OE,且OE=DE.求OE所在的直线解析式.
如图,平面直角坐标系中,O为坐标原点,已知直线y=$\frac{1}{2}$x+5分别与x,y轴相交于点F、D,点E在线段DF上,连接OE,且OE=DE.求OE所在的直线解析式.