题目内容
11.设方程x2+x-1=0的两根是x1,x2,求4x15+10x23的值.分析 先根据一元二次方程根与系数的关系确定出x1与x2的两根之积与两根之和的值,代入所求的代数式即可得到结果.
解答 解:x1+x2=-1,x1x2=-1,
4x15+10x23
=4×(${x}_{1}^{2}$×${x}_{1}^{2}$×x1)+10×(${x}_{2}^{2}$×x2)
=4×$(1{-x}_{1})^{2}$×x1+10×(1-x2)×x2
=$4({x}_{1}^{2}-{2x}_{1}+1){×x}_{1}+10{(x}_{2}{+x}_{2}-1)$
=4(1-x1-2x1+1)×x1+10(2x2-1)
=4(2-3x1)×x1+10(2x2-1)
=4(2x1+3x1-3)+10(2x2-1)
=20x1-12+20x2-10
=20(x1+x2)-22
=-20-22
=-42.
点评 此题考查了根与系数的关系,常用根与系数的关系解决以下问题:①不解方程,判断两个数是不是一元二次方程的两个根.②已知方程及方程的一个根,求另一个根及未知数.③不解方程求关于根的式子的值,如求,x12+x22等等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.小明、小联、小豪人一起玩“剪刀、石头、布”的游戏.每一局三人同时出“剪刀、石头、布”中的一种手势.则小明只赢一人的概率为( )
| A. | $\frac{2}{9}$ | B. | $\frac{4}{9}$ | C. | $\frac{2}{27}$ | D. | $\frac{4}{27}$ |
6.若0°<α<90°,那么,以sinα、cosα、tanα•cotα为三边的△ABC的内切圆半径与外接圆半径之和是( )
| A. | 2sinα•cosα | B. | $\frac{tanα+cotα}{2}$ | C. | $\frac{sinα+cosα}{2}$ | D. | $\frac{1}{sinα•cosα}$ |
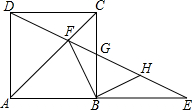 如图,E为正方形ABCD的边AB延长线上一点,DE交AC于点F,交BC于点G,H为GE的中点,求证:FB⊥BH.
如图,E为正方形ABCD的边AB延长线上一点,DE交AC于点F,交BC于点G,H为GE的中点,求证:FB⊥BH.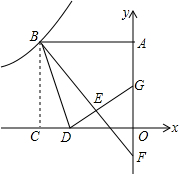 如图,正方形OABC的顶点A在y轴的正半轴上,顶点C在x轴的负半轴上,反比例函数y=-$\frac{9}{x}$在第二象限的图象经过点B,点D坐标为(-2,0),将正方形沿BD翻折,使点C落在E处,分别延长BE、DE角y轴于点F和G,则线段FG的长度是$\frac{5}{2}$.
如图,正方形OABC的顶点A在y轴的正半轴上,顶点C在x轴的负半轴上,反比例函数y=-$\frac{9}{x}$在第二象限的图象经过点B,点D坐标为(-2,0),将正方形沿BD翻折,使点C落在E处,分别延长BE、DE角y轴于点F和G,则线段FG的长度是$\frac{5}{2}$.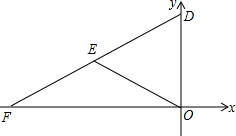 如图,平面直角坐标系中,O为坐标原点,已知直线y=$\frac{1}{2}$x+5分别与x,y轴相交于点F、D,点E在线段DF上,连接OE,且OE=DE.求OE所在的直线解析式.
如图,平面直角坐标系中,O为坐标原点,已知直线y=$\frac{1}{2}$x+5分别与x,y轴相交于点F、D,点E在线段DF上,连接OE,且OE=DE.求OE所在的直线解析式.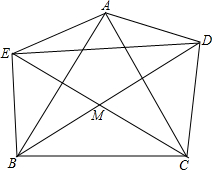 如图,△ABC中,D,E是△ABC外两点,M是△ABC内一点.若AE=BE,AD=DC,∠DEM=$\frac{1}{2}$∠AEB,∠EDM=$\frac{1}{2}$∠ADC.求证:MB=MC.
如图,△ABC中,D,E是△ABC外两点,M是△ABC内一点.若AE=BE,AD=DC,∠DEM=$\frac{1}{2}$∠AEB,∠EDM=$\frac{1}{2}$∠ADC.求证:MB=MC.