题目内容
16.⊙O的内接正三角形与正六边形的面积之比为( )| A. | $\sqrt{2}$:1 | B. | 1:$\sqrt{3}$ | C. | 1:2 | D. | 1:$\sqrt{2}$ |
分析 设⊙O的半径为R,作OM⊥BC于M,ON⊥CF于N,连接OB、OC、OF;则BM=CM=$\frac{1}{2}$BC,CN=FN=$\frac{1}{2}$CF,由⊙O的内接正三角形的性质得出∠OBC=30°,得出OM=$\frac{1}{2}$R,BM=$\frac{\sqrt{3}}{2}$R,得出BC=$\sqrt{3}$R,求出△ABC的面积=$\frac{1}{2}$BC•OM×3=$\frac{3\sqrt{3}}{4}$R2,同理得出CN=$\frac{1}{2}$R,ON=$\frac{\sqrt{3}}{2}$R,CF=R,正六边形ADBECF的面积=$\frac{1}{2}$CF•ON×6=$\frac{3\sqrt{3}}{2}$R2,即可得出结果.
解答 解:设⊙O的半径为R,如图所示: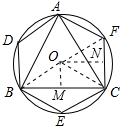
作OM⊥BC于M,ON⊥CF于N,连接OB、OC、OF;
则BM=CM=$\frac{1}{2}$BC,CN=FN=$\frac{1}{2}$CF,
∵△ABC是⊙O的内接正三角形,
∴∠OBC=30°,
∴OM=$\frac{1}{2}$R,BM=$\frac{\sqrt{3}}{2}$R,
∴BC=$\sqrt{3}$R,
∴△ABC的面积=$\frac{1}{2}$BC•OM×3=$\frac{1}{2}$×$\sqrt{3}$R×$\frac{1}{2}$R×3=$\frac{3\sqrt{3}}{4}$R2,
同理:CN=$\frac{1}{2}$R,ON=$\frac{\sqrt{3}}{2}$R,CF=R,
∴正六边形ADBECF的面积=$\frac{1}{2}$CF•ON×6=$\frac{1}{2}$×R×$\frac{\sqrt{3}}{2}$R×6=$\frac{3\sqrt{3}}{2}$R2,
∴⊙O的内接正三角形与正六边形的面积之比为1:2.
故选:C.
点评 本题考查了圆的内接正三角形与正六边形的性质、正三角形与正六边形的面积的计算、垂径定理;熟练掌握圆的内接正三角形与正六边形的性质,并能进行推理计算是解决问题的关键.

 新思维寒假作业系列答案
新思维寒假作业系列答案| A. | -7 | B. | -1或-7 | C. | -13或5 | D. | 5 |
| A. | 2sinα•cosα | B. | $\frac{tanα+cotα}{2}$ | C. | $\frac{sinα+cosα}{2}$ | D. | $\frac{1}{sinα•cosα}$ |
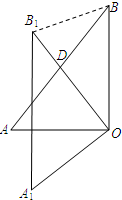 如图,△AOB中,∠AOB=90°,AO=6,BO=8,将△AOB绕顶点O逆时针旋转到△A1OB1处,此时线段OB1与AB的交点D恰好为AB的中点,则线段BB1的长度为$\frac{8\sqrt{10}}{5}$.
如图,△AOB中,∠AOB=90°,AO=6,BO=8,将△AOB绕顶点O逆时针旋转到△A1OB1处,此时线段OB1与AB的交点D恰好为AB的中点,则线段BB1的长度为$\frac{8\sqrt{10}}{5}$.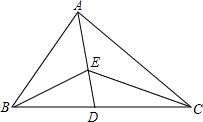 如图,AD为△ABC的角平分线,点E在AD上.
如图,AD为△ABC的角平分线,点E在AD上.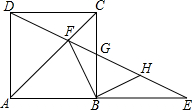 如图,E为正方形ABCD的边AB延长线上一点,DE交AC于点F,交BC于点G,H为GE的中点,求证:FB⊥BH.
如图,E为正方形ABCD的边AB延长线上一点,DE交AC于点F,交BC于点G,H为GE的中点,求证:FB⊥BH.