题目内容
9.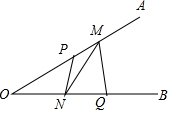 已知∠AOB=30°,点P、Q分别是边OA、OB上的定点,OP=3,OQ=4,点M、N是分别是边OA、OB上的动点,则折线P-N-M-Q长度的最小值是5.
已知∠AOB=30°,点P、Q分别是边OA、OB上的定点,OP=3,OQ=4,点M、N是分别是边OA、OB上的动点,则折线P-N-M-Q长度的最小值是5.
分析 作P关于OB的对称点P′,作Q关于OA的对称点Q′,连接P′Q′,即为折线P-N-M-Q长度的最小值.
解答  解:作P关于OB的对称点P′,作Q关于OA的对称点Q′,
解:作P关于OB的对称点P′,作Q关于OA的对称点Q′,
连接P′Q′,即为折线P-N-M-Q长度的最小值.
根据轴对称的定义可知:∠NOP′=∠AOB=30°,∠OPP′=60°,
∴△OPP′为等边三角形,△OQQ′为等边三角形,
∴∠P′OQ′=90°,
∴在Rt△P′OQ′中,
P′Q′=$\sqrt{{3}^{2}+{4}^{2}}$=5.
故答案为5.
点评 本题考查了轴对称--最短路径问题,根据轴对称的定义,找到相等的线段,得到等边三角形是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


 如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.求证:BE=CE (要求:不用三角形全等的方法)
如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.求证:BE=CE (要求:不用三角形全等的方法)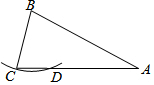 如图,在△ABC中,AB=AC=2BC,以点B为圆心,BC长为半径作弧,与AC交于点D.若AC=4,则线段CD的长为1.
如图,在△ABC中,AB=AC=2BC,以点B为圆心,BC长为半径作弧,与AC交于点D.若AC=4,则线段CD的长为1. 如图,将一个多边形按图所示减掉一个角,所得多边形的内角和为1800°,求原多边形的边数.
如图,将一个多边形按图所示减掉一个角,所得多边形的内角和为1800°,求原多边形的边数.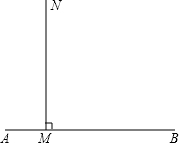 已知如图:射线MN⊥AB于点M,点C从M出发,以1cm/s的速度沿射线MN运动,AM=1,MB=4,设运动时间为ts,①当△ABC为等腰三角形时,求t的值;②当△ABC为直角三角形时,求t的值;③点C在运动的过程中,若△ABC为钝角三角形,则t的取值范围是0<t<2;若△ABC为锐角三角形,则t的取值范围是t>2.
已知如图:射线MN⊥AB于点M,点C从M出发,以1cm/s的速度沿射线MN运动,AM=1,MB=4,设运动时间为ts,①当△ABC为等腰三角形时,求t的值;②当△ABC为直角三角形时,求t的值;③点C在运动的过程中,若△ABC为钝角三角形,则t的取值范围是0<t<2;若△ABC为锐角三角形,则t的取值范围是t>2. 如图,直线y=2x+2$\sqrt{3}$与x、y轴分别交于A、B两点,以OB为边在y轴左侧作等边△OBC,将△OBC沿y轴上下平移,使点C的对应点C′恰好落在直线AB上,则点C'的坐标为(-3,-6+2$\sqrt{3}$).
如图,直线y=2x+2$\sqrt{3}$与x、y轴分别交于A、B两点,以OB为边在y轴左侧作等边△OBC,将△OBC沿y轴上下平移,使点C的对应点C′恰好落在直线AB上,则点C'的坐标为(-3,-6+2$\sqrt{3}$).