题目内容
4.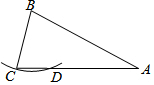 如图,在△ABC中,AB=AC=2BC,以点B为圆心,BC长为半径作弧,与AC交于点D.若AC=4,则线段CD的长为1.
如图,在△ABC中,AB=AC=2BC,以点B为圆心,BC长为半径作弧,与AC交于点D.若AC=4,则线段CD的长为1.
分析 连结BD,然后依据等边对等角的性质证明∠C=∠BDC,∠C=∠CBA,从而可证明△BCD∽△ACB,最后依据相似三角形的性质求解即可.
解答 解:如图所示:连结BD.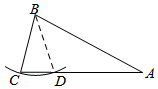
∵AB=AC=2BC,AC=4,
∴BC=2.
∵BC=BD,
∴∠C=∠BDC.
∵AB=AC,
∴∠C=∠CBA.
∴∠BDC=∠CBA.
又∵∠C=∠C,
∴△BCD∽△ACB.
∴$\frac{CD}{CB}$=$\frac{CB}{AC}$即$\frac{CD}{2}$=$\frac{2}{4}$,解得:CD=1.
故答案为:1.
点评 本题主要考查的是相似三角形的性质和判定、等腰三角形的性质,熟练掌握相关知识是解题的关键.

练习册系列答案
相关题目
13.下列函数关系不是一次函数的是( )
| A. | 汽车以120Km/h的速度匀速行驶,行驶路程y(Km)与时间t(h)之间的关系 | |
| B. | 等腰三角形顶角y与底角x间的关系 | |
| C. | 高为4cm的圆锥体积y (cm3)与底面半径x (cm)的关系 | |
| D. | 一棵树现在高50cm,每月长高3cm,x个月后这棵树的高度y (cm)与生长月数x(月)之间的关系 |
14.据浙江电商网统计,2014年嘉兴市网络零售额678.89亿元,列全省第三.其中678.89亿元可用科学记数法表示为( )
| A. | 678.89×108元 | B. | 67.889×109元 | C. | 6.7889×109元 | D. | 6.7889×1010元 |
 如图,△ABC中,DE∥FG∥BC.
如图,△ABC中,DE∥FG∥BC. 如图所示,一直按此规律进行下去,试求第10个直角三角形的斜边长为多少?第n个直角三角形的斜边长又为多少?
如图所示,一直按此规律进行下去,试求第10个直角三角形的斜边长为多少?第n个直角三角形的斜边长又为多少?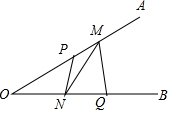 已知∠AOB=30°,点P、Q分别是边OA、OB上的定点,OP=3,OQ=4,点M、N是分别是边OA、OB上的动点,则折线P-N-M-Q长度的最小值是5.
已知∠AOB=30°,点P、Q分别是边OA、OB上的定点,OP=3,OQ=4,点M、N是分别是边OA、OB上的动点,则折线P-N-M-Q长度的最小值是5.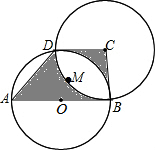 如图,AB为圆O的直径,点D在圆O上,在梯形ABCD中:
如图,AB为圆O的直径,点D在圆O上,在梯形ABCD中: