题目内容
7.如图,CA=CB,CD=CE,∠ACB=∠DCE=α,连AD,BE相交于H,连CH(1)如图1,当α=60°时,求∠AHE与∠BHC;
(2)如图2,当α=90°时,求∠AHE与∠BHC;
(3)如图3,当α为锐角时,求∠AHE与∠BHC;
(4)如图4,当α为钝角时,求∠AHE与∠BHC.

分析 (1)只要证明△ACD≌△BCE,A、B、H、C四点共圆,即可解决问题.
(2)(3)(4)方法类似(1).
解答 解:(1)如图1中,
∵CA=CB,CD=CE,∠ACB=∠DCE=α,α=60°,
∴△ABC,△CDE都是等边三角形,
∴∠BAC=∠ACB=60°,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE,
∴∠CAD=∠CBE,
∵∠ADC=∠BDH,
∴∠BHD=∠ACD=60°,
∴∠AHE=120°,A、B、H、C四点共圆,
∴∠BHC=180°-∠BAC=120°.
(2)如图2中,
∵CA=CB,CD=CE,∠ACB=∠DCE=α,α=90°,
∴△ABC,△CDE都是等腰直角三角形,∠ACD=∠BCE,
∴∠BAC=∠ABC=45°,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE,
∴∠CAD=∠CBE,
∴A、B、H、C四点共圆,
∴∠BHA=∠ACB=90°,∠BHC=180°-∠BAC=135°
∴∠AHE=180°-∠BHA=90°.
(3)如图3中,
∵CA=CB,CD=CE,∠ACB=∠DCE=α,
∠ACD=∠BCE,
∴∠BAC=90°-$\frac{1}{2}$α,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE,
∴∠CAD=∠CBE,
∴A、B、H、C四点共圆,
∴∠BHA=∠ACB=α,
∴∠AHE=∠ACB=α,∠BHC=180°-∠BAC=90°+$\frac{1}{2}$α.
(4)如图4中,
∵CA=CB,CD=CE,∠ACB=∠DCE=α,
∠ACD=∠BCE,
∴∠BAC=90°-$\frac{1}{2}$α,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE,
∴∠CAD=∠CBE,
∴A、H、B、C四点共圆,
∴∠AHE=180°-∠ACB=180°-α,∠BHC=∠BAC=90°-$\frac{1}{2}$α.
点评 本题考查全等三角形的判定和性质、四点共圆等知识,解题的关键是四点共圆的判定和性质,难点是用到四点共圆的判定.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $\frac{10}{x}$=$\frac{3}{40}$ | B. | $\frac{10}{x}$=$\frac{1}{40}$ | C. | $\frac{10}{x}$=$\frac{1}{3}$ | D. | $\frac{10}{x+10}$=$\frac{3}{40}$ |
| 月使用费(元) | 主叫限定时间(分钟) | 主叫超时费/(元/分) | 被叫 | |
| 方式一 | 58 | 150 | 0.25 | 免费 |
| 方式二 | 88 | 350 | 0.19 | 免费 |
| A. | 方式一 | B. | 方式二 | C. | 两种方式一样 | D. | 无法确定 |
| A. | 50 | B. | 40 | C. | 30 | D. | 20 |
| -0.8 | +1 | -1.2 | -0.1 | -0.6 | +0.6 | -0.3 | -0.2 |
(2)这个小组男生的达标率为多少?(达标率=$\frac{达标人数}{总人数}$)
(3)这个小组男生的平均成绩是多少秒?

 如图,AB是⊙O的直径,弦CD⊥AB于点M,连结CO,CB.
如图,AB是⊙O的直径,弦CD⊥AB于点M,连结CO,CB.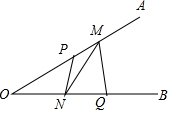 已知∠AOB=30°,点P、Q分别是边OA、OB上的定点,OP=3,OQ=4,点M、N是分别是边OA、OB上的动点,则折线P-N-M-Q长度的最小值是5.
已知∠AOB=30°,点P、Q分别是边OA、OB上的定点,OP=3,OQ=4,点M、N是分别是边OA、OB上的动点,则折线P-N-M-Q长度的最小值是5.