题目内容
1.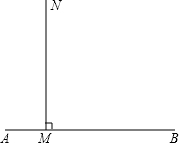 已知如图:射线MN⊥AB于点M,点C从M出发,以1cm/s的速度沿射线MN运动,AM=1,MB=4,设运动时间为ts,①当△ABC为等腰三角形时,求t的值;②当△ABC为直角三角形时,求t的值;③点C在运动的过程中,若△ABC为钝角三角形,则t的取值范围是0<t<2;若△ABC为锐角三角形,则t的取值范围是t>2.
已知如图:射线MN⊥AB于点M,点C从M出发,以1cm/s的速度沿射线MN运动,AM=1,MB=4,设运动时间为ts,①当△ABC为等腰三角形时,求t的值;②当△ABC为直角三角形时,求t的值;③点C在运动的过程中,若△ABC为钝角三角形,则t的取值范围是0<t<2;若△ABC为锐角三角形,则t的取值范围是t>2.
分析 ①分CB=AB、AB=AC和AC=BC三种情况,根据等腰三角形的性质和勾股定理计算即可;
②根据勾股定理列式计算;
③由②的结论结合图形解答.
解答 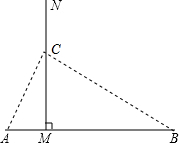 解:①当CB=AB时,
解:①当CB=AB时,
在Rt△MCB,BC=5,BM=4,
由勾股定理得:MC=3,
则t=3s;
当AB=AC时,
在Rt△MCA,AM=1,AC=5,
由勾股定理得:MC=$\sqrt{{5}^{2}-{1}^{2}}$=2$\sqrt{6}$,
则t=2$\sqrt{6}$s;
当AC=BC时,C在AB的垂直平分线上,与条件不合;
∴当t=3s或2$\sqrt{6}$s时,△ABC为等腰三角形;
②∵由题意∠ACB=90°时,
∴AC2+BC2=AB2,
设CM=x,在Rt△MCB中由勾股定理得:BC2=x2+42,
在Rt△MCA中,由勾股定理得:AC2=x2+12,
∴x2+42+x2+12=52,解得x=2,
∴t=2s;
③∵当t=2时,△ABC为直角三角形,
∴0<t<2时,△ABC为钝角三角形;
t>2时,△ABC为锐角三角形.
故答案为:0<t<2;t>2.
点评 本题考查的是勾股定理的应用,如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2,注意分情况讨论思想的运用.

练习册系列答案
相关题目
11.某工厂要招聘A、B两个工种的工人120人,A、B两个工种的工人的月工资分别为1500元和3000元,现要求B工种的人数不少于A工种人数的2倍,要使工厂每月所付的工资总额最少,那么工厂招聘A种工人的人数至多是( )人.
| A. | 50 | B. | 40 | C. | 30 | D. | 20 |
13.下列函数关系不是一次函数的是( )
| A. | 汽车以120Km/h的速度匀速行驶,行驶路程y(Km)与时间t(h)之间的关系 | |
| B. | 等腰三角形顶角y与底角x间的关系 | |
| C. | 高为4cm的圆锥体积y (cm3)与底面半径x (cm)的关系 | |
| D. | 一棵树现在高50cm,每月长高3cm,x个月后这棵树的高度y (cm)与生长月数x(月)之间的关系 |
 如图,△ABC中,DE∥FG∥BC.
如图,△ABC中,DE∥FG∥BC.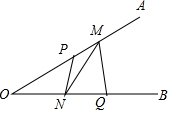 已知∠AOB=30°,点P、Q分别是边OA、OB上的定点,OP=3,OQ=4,点M、N是分别是边OA、OB上的动点,则折线P-N-M-Q长度的最小值是5.
已知∠AOB=30°,点P、Q分别是边OA、OB上的定点,OP=3,OQ=4,点M、N是分别是边OA、OB上的动点,则折线P-N-M-Q长度的最小值是5.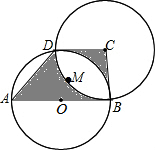 如图,AB为圆O的直径,点D在圆O上,在梯形ABCD中:
如图,AB为圆O的直径,点D在圆O上,在梯形ABCD中: 如图1,点D位于△ABC边AC上,已知AB是AD与AC的比例中项.
如图1,点D位于△ABC边AC上,已知AB是AD与AC的比例中项.