题目内容
18.已知△ABC的两边AB、AC的长是关于x的一元二次方程x2-(2k+1)x+k2+k=0的两个实数根,第三边BC的长为5,当△ABC是等腰三角形时,则k的值为5或4.分析 先计算判别式的值得到△=1,则可利用求根公式得到方程的解为x1=k+1,x2=k,则得到AB和AC的乘为k+1,k,然后根据等腰三角形的性质得到k+1=5或k=5,从而可确定k的值.
解答 解:△=(2k+1)2-4(k2+k)=1,
所以x=$\frac{2k+1±1}{2}$,解得x1=k+1,x2=k,
当k+1=5时,解得k=4,此时△ABC是等腰三角形
当k=5时,此时△ABC是等腰三角形,
即k为值为5或4.
故答案为5或4.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.也考查了等腰三角形的性质.

练习册系列答案
相关题目
8.体育课上,全班男同学进行了100米测验,达标成绩为15秒,如表是某小组8名男生的成绩记录,其中“+“表示成绩大于15秒.
问:(1)这个小组男生最优秀的成绩是多少秒?最差的成绩是多少秒?
(2)这个小组男生的达标率为多少?(达标率=$\frac{达标人数}{总人数}$)
(3)这个小组男生的平均成绩是多少秒?
| -0.8 | +1 | -1.2 | -0.1 | -0.6 | +0.6 | -0.3 | -0.2 |
(2)这个小组男生的达标率为多少?(达标率=$\frac{达标人数}{总人数}$)
(3)这个小组男生的平均成绩是多少秒?
13.下列函数关系不是一次函数的是( )
| A. | 汽车以120Km/h的速度匀速行驶,行驶路程y(Km)与时间t(h)之间的关系 | |
| B. | 等腰三角形顶角y与底角x间的关系 | |
| C. | 高为4cm的圆锥体积y (cm3)与底面半径x (cm)的关系 | |
| D. | 一棵树现在高50cm,每月长高3cm,x个月后这棵树的高度y (cm)与生长月数x(月)之间的关系 |
7.下列命题中,正确的个数是( )
(1)三点确定一个圆;
(2)平分弦的直径垂直于弦;
(3)相等的圆心角所对的弧相等;
(4)正五边形是轴对称图形.
(1)三点确定一个圆;
(2)平分弦的直径垂直于弦;
(3)相等的圆心角所对的弧相等;
(4)正五边形是轴对称图形.
| A. | 1 个 | B. | 2 个 | C. | 3 个 | D. | 4 个 |
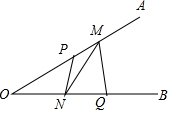 已知∠AOB=30°,点P、Q分别是边OA、OB上的定点,OP=3,OQ=4,点M、N是分别是边OA、OB上的动点,则折线P-N-M-Q长度的最小值是5.
已知∠AOB=30°,点P、Q分别是边OA、OB上的定点,OP=3,OQ=4,点M、N是分别是边OA、OB上的动点,则折线P-N-M-Q长度的最小值是5.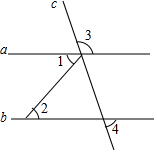 如图,若∠1=40°30′,∠2=40°30′,∠3=120°,则∠4=60°.
如图,若∠1=40°30′,∠2=40°30′,∠3=120°,则∠4=60°. 如图1,点D位于△ABC边AC上,已知AB是AD与AC的比例中项.
如图1,点D位于△ABC边AC上,已知AB是AD与AC的比例中项.