题目内容
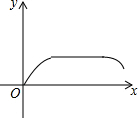
8.如图:Rt△ABE、Rt△DCE与矩形MNPQ的边BE、EC、NP都在直线m上,BC=NP=6,直角边AB=DE=MN=2,∠ECD=45°,Rt△ABE与Rt△DCE组合成图形ABCDE,图形ABCDE向右运动至点C和P重合为止,设运动距离是x,图形ABCDE与矩形MNPQ重合面积是y,则y关于x的函数图象应当是( )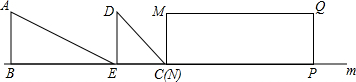
| A. | 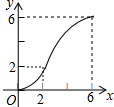 | B. | 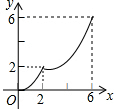 | C. | 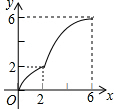 | D. |  |
分析 根据题意可得各段对应的函数解析,从而可以得到各段的函数图象,从而可以得到哪个选项是正确的.
解答 解:设∠AEB=α,由题意可得,
当点D与点M重合的过程中,
y=$\frac{x•x•tan45°}{2}=\frac{{x}^{2}}{2}$(0≤x≤2);
当点C与点P重合的过程中,
y=$\frac{2×2}{2}+\frac{(x-2)•(x-2)•tanα}{2}$=$2+\frac{tanα}{2}(x-2)^{2}$,
由上可得,刚开始函数图象开口向上的抛物线,然后也是开口向上的抛物线,
故选D.
点评 本题考查动点问题的函数图象,解题的关键是明确题意,写出各段对应的函数解析式,明确各段对应的函数图象.

练习册系列答案
相关题目
10. 如图,在平面直角坐标系中,已知点A(2,0),B(0,3),如果将线段AB绕点B顺时针旋转90°至CB,那么点C的坐标是( )
如图,在平面直角坐标系中,已知点A(2,0),B(0,3),如果将线段AB绕点B顺时针旋转90°至CB,那么点C的坐标是( )
 如图,在平面直角坐标系中,已知点A(2,0),B(0,3),如果将线段AB绕点B顺时针旋转90°至CB,那么点C的坐标是( )
如图,在平面直角坐标系中,已知点A(2,0),B(0,3),如果将线段AB绕点B顺时针旋转90°至CB,那么点C的坐标是( )| A. | (-3,2) | B. | (-3,1) | C. | (2,1) | D. | (-2,1) |
17. 如图,以BC为直径作半圆$\widehat{BAC}$,A为半圆的中点,现将半圆连同直径绕点A顺时针旋转45°,记点B、C的对应点分别为B′、C′,连接B′C,BC′,则$\frac{B′C}{BC′}$=( )
如图,以BC为直径作半圆$\widehat{BAC}$,A为半圆的中点,现将半圆连同直径绕点A顺时针旋转45°,记点B、C的对应点分别为B′、C′,连接B′C,BC′,则$\frac{B′C}{BC′}$=( )
 如图,以BC为直径作半圆$\widehat{BAC}$,A为半圆的中点,现将半圆连同直径绕点A顺时针旋转45°,记点B、C的对应点分别为B′、C′,连接B′C,BC′,则$\frac{B′C}{BC′}$=( )
如图,以BC为直径作半圆$\widehat{BAC}$,A为半圆的中点,现将半圆连同直径绕点A顺时针旋转45°,记点B、C的对应点分别为B′、C′,连接B′C,BC′,则$\frac{B′C}{BC′}$=( )| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{2}{5}$ | C. | $\sqrt{2}-1$ | D. | 2$-\sqrt{2}$ |
 如图,直线a∥b,∠1=110°,∠2=65°,则∠3的度数为45°.
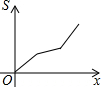
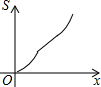
如图,直线a∥b,∠1=110°,∠2=65°,则∠3的度数为45°.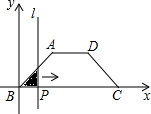 如图,在四边形ABCD中,AD∥BC,AB=DC,以点B为原点,BC边所在的直线为x轴建立平面直角坐标系,直线l与y轴重合且向右平移,若其扫过的面积(阴影部分)为S,设向右平移的距离BP为x,则S关于x的函数图象大致是( )
如图,在四边形ABCD中,AD∥BC,AB=DC,以点B为原点,BC边所在的直线为x轴建立平面直角坐标系,直线l与y轴重合且向右平移,若其扫过的面积(阴影部分)为S,设向右平移的距离BP为x,则S关于x的函数图象大致是( )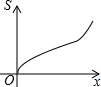

 如图,矩形MDBN从B点匀速向右运动,当B点与C点重合时停止,设移动的时间为x,两图形重合的面积为y,则y关于x的函数图象是( )
如图,矩形MDBN从B点匀速向右运动,当B点与C点重合时停止,设移动的时间为x,两图形重合的面积为y,则y关于x的函数图象是( )


 已知二次函数y=2x2-x-3.
已知二次函数y=2x2-x-3.