题目内容
19.若(m+75)2=851012,则(m+65)(m+85)=850912.分析 把原式化为平方差的形式,根据平方差公式把原式进行变形,代入已知数据计算即可.
解答 解:(m+65)(m+85)
=(m+75-10)(m+75+10)
=(m+75)2-100
=851012-100
=850912,
故答案为:850912.
点评 本题考查的是多项式乘多项式的计算,掌握平方差公式:(a+b)(a-b)=a2-b2是解题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
7.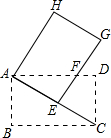 将矩形ABCD绕点A逆时针旋转得到矩形AEGH,若点E恰好落在AC上,EG交AD于点F,如图,已知AB=3,AC=5,则FG的长为( )
将矩形ABCD绕点A逆时针旋转得到矩形AEGH,若点E恰好落在AC上,EG交AD于点F,如图,已知AB=3,AC=5,则FG的长为( )
 将矩形ABCD绕点A逆时针旋转得到矩形AEGH,若点E恰好落在AC上,EG交AD于点F,如图,已知AB=3,AC=5,则FG的长为( )
将矩形ABCD绕点A逆时针旋转得到矩形AEGH,若点E恰好落在AC上,EG交AD于点F,如图,已知AB=3,AC=5,则FG的长为( )| A. | 2 | B. | $\frac{7}{4}$ | C. | $\frac{9}{4}$ | D. | 4 |
4.下列运算正确的是( )
| A. | (-2x-1)(2x-1)=1-4x2 | B. | 2x(x2-2x-14)=2x3-4x2+28x | ||
| C. | (x-2y)2=x2-2xy+4y2 | D. | (x+1)(x-4)=x2-4 |
9.下列等式成立的是( )
| A. | $\frac{1}{a}$$+\frac{2}{b}$=$\frac{3}{a+b}$ | B. | $\frac{ab}{ab-{b}^{2}}$=$\frac{a}{a-b}$ | C. | $\frac{2}{2a+b}$=$\frac{1}{-a+b}$ | D. | $\frac{a}{-a+b}$=-$\frac{a}{a+b}$ |
 如图,C、D是线段AB上两点,且AC=BD=$\frac{1}{6}$AB=1,点P是线段CD上一个动点,在AB同侧分别作等边△PAE和等边△PBF,M为线段EF的中点.在点P从点C移动到点D时,点M运动的路径长度为2.
如图,C、D是线段AB上两点,且AC=BD=$\frac{1}{6}$AB=1,点P是线段CD上一个动点,在AB同侧分别作等边△PAE和等边△PBF,M为线段EF的中点.在点P从点C移动到点D时,点M运动的路径长度为2.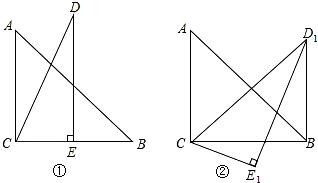
 如图,菱形ABCD中,两条对角线长AC=8,BD=6,则菱形ABCD的面积为24.
如图,菱形ABCD中,两条对角线长AC=8,BD=6,则菱形ABCD的面积为24.