题目内容
10. 如图,在平面直角坐标系中,已知点A(2,0),B(0,3),如果将线段AB绕点B顺时针旋转90°至CB,那么点C的坐标是( )
如图,在平面直角坐标系中,已知点A(2,0),B(0,3),如果将线段AB绕点B顺时针旋转90°至CB,那么点C的坐标是( )| A. | (-3,2) | B. | (-3,1) | C. | (2,1) | D. | (-2,1) |
分析 作CD⊥y轴于点D,如图,根据旋转的性质得∠ABC=90°,BC=BA,再利用等角的余角相等得到∠CBD=∠A,则可证明△ABO≌△BCD得到BD=OA=2,CD=OB=3,然后根据第二象限内点的坐标特征写出C点坐标.
解答 解:作CD⊥y轴于点D,如图,
∵A(2,0),B(0,3),
∴OA=2,OB=3,
∵线段AB绕点B顺时针旋转90°至CB,
∴∠ABC=90°,BC=BA,
∵∠ABO+∠A=90°,∠ABO+∠CBD=90°,
∴∠CBD=∠A,
在△ABO和△BCD中
$\left\{\begin{array}{l}{∠AOB=∠BDC}\\{∠A=∠C}\\{AB=BC}\end{array}\right.$,
∴△ABO≌△BCD,
∴BD=OA=2,CD=OB=3,
∴OD=OB-BD=3-2=1,
∴C点坐标为(-3,1).
故选B.
点评 本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.解决本题的关键是作CD⊥y轴于点D后求出CD和OD的长.

练习册系列答案
相关题目
18.下列不等式组中解集为x<1的是( )
| A. | $\left\{\begin{array}{l}x<1\\ x<2\end{array}\right.$ | B. | $\left\{\begin{array}{l}x<1\\ x>2\end{array}\right.$ | C. | $\left\{\begin{array}{l}x>1\\ x>2\end{array}\right.$ | D. | $\left\{\begin{array}{l}x>1\\ x<2\end{array}\right.$ |
5.下列运算正确的是( )
| A. | a•a2=a2 | B. | (ab)2=ab2 | C. | a6÷a2=a4 | D. | (a2)3=a5 |
15.下列运算正确的是( )
| A. | 4m-m=3 | B. | -(m+2n)=-m+2n | C. | (-m3)2=m9 | D. | 2m2•m3=2m5 |
7.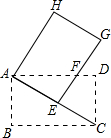 将矩形ABCD绕点A逆时针旋转得到矩形AEGH,若点E恰好落在AC上,EG交AD于点F,如图,已知AB=3,AC=5,则FG的长为( )
将矩形ABCD绕点A逆时针旋转得到矩形AEGH,若点E恰好落在AC上,EG交AD于点F,如图,已知AB=3,AC=5,则FG的长为( )
 将矩形ABCD绕点A逆时针旋转得到矩形AEGH,若点E恰好落在AC上,EG交AD于点F,如图,已知AB=3,AC=5,则FG的长为( )
将矩形ABCD绕点A逆时针旋转得到矩形AEGH,若点E恰好落在AC上,EG交AD于点F,如图,已知AB=3,AC=5,则FG的长为( )| A. | 2 | B. | $\frac{7}{4}$ | C. | $\frac{9}{4}$ | D. | 4 |
 如图,四边形ABCD是⊙O的内接四边形,已知∠BOD=120°,则∠BCD的度数为120°.
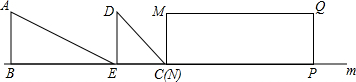
如图,四边形ABCD是⊙O的内接四边形,已知∠BOD=120°,则∠BCD的度数为120°. 如图,C、D是线段AB上两点,且AC=BD=$\frac{1}{6}$AB=1,点P是线段CD上一个动点,在AB同侧分别作等边△PAE和等边△PBF,M为线段EF的中点.在点P从点C移动到点D时,点M运动的路径长度为2.
如图,C、D是线段AB上两点,且AC=BD=$\frac{1}{6}$AB=1,点P是线段CD上一个动点,在AB同侧分别作等边△PAE和等边△PBF,M为线段EF的中点.在点P从点C移动到点D时,点M运动的路径长度为2.