题目内容
20.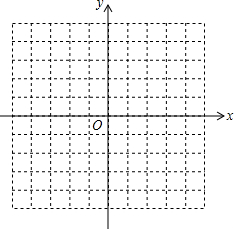 已知二次函数y=2x2-x-3.
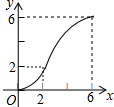
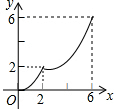
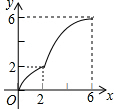
已知二次函数y=2x2-x-3.(1)求函数图象的顶点坐标,与坐标轴交点坐标,并画出函数大致图象;
(2)根据图象直接回答:当x为何值时,y<0?当x为何值时y>-3?
分析 (1)把二次函数的解析式化成顶点式,即可得出顶点坐标;求出当x=0时y的值以及y=0时x的值即可;
(2)根据函数的图象容易得出结果.
解答 解:(1) ∵y=2x2-x-3=2(x-$\frac{1}{4}$)2-$\frac{25}{8}$,
∵y=2x2-x-3=2(x-$\frac{1}{4}$)2-$\frac{25}{8}$,
∴顶点坐标为$(\frac{1}{4},-\frac{25}{8})$,
当x=0时,y=-3;
当y=0时,2x2-x-3=0,
解得:x=-1,或x=$\frac{3}{2}$,
∴二次函数的图象与y轴的交点坐标为(0,-3),与x轴的交点坐标为($\frac{3}{2}$,0);
图象如图所示:
(2)当$-1<x<\frac{3}{2}$,y<0;
当x<0或$x>\frac{1}{2}$,y>-2.
点评 本题考查了二次函数的图象、抛物线与x轴的交点、二次函数的顶点式、二次函数的图象;熟练掌握二次函数的图象,把抛物线化成顶点式是解决问题的关键.

练习册系列答案
相关题目
15.若M(-2,y1),N(-1,y2),P(2,y3)三点都在函数y=$\frac{k}{x}$(k<0)的图象上,则y1,y2,y3的大小关系是( )
| A. | y3>y1>y2 | B. | y3>y2>y1 | C. | y1>y2>y3 | D. | y2>y1>y3 |
9.下列等式成立的是( )
| A. | $\frac{1}{a}$$+\frac{2}{b}$=$\frac{3}{a+b}$ | B. | $\frac{ab}{ab-{b}^{2}}$=$\frac{a}{a-b}$ | C. | $\frac{2}{2a+b}$=$\frac{1}{-a+b}$ | D. | $\frac{a}{-a+b}$=-$\frac{a}{a+b}$ |
10.在八边形内任取一点,把这个点与八边形各顶点分别连接可得到几个三角形( )
| A. | 5个 | B. | 6个 | C. | 7个 | D. | 8个 |
 如图,菱形ABCD中,两条对角线长AC=8,BD=6,则菱形ABCD的面积为24.
如图,菱形ABCD中,两条对角线长AC=8,BD=6,则菱形ABCD的面积为24.