题目内容
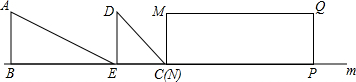
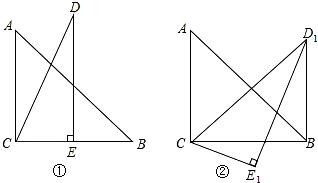
3.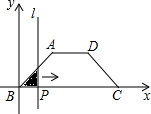 如图,在四边形ABCD中,AD∥BC,AB=DC,以点B为原点,BC边所在的直线为x轴建立平面直角坐标系,直线l与y轴重合且向右平移,若其扫过的面积(阴影部分)为S,设向右平移的距离BP为x,则S关于x的函数图象大致是( )
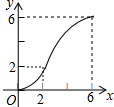
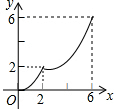
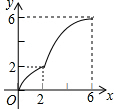
如图,在四边形ABCD中,AD∥BC,AB=DC,以点B为原点,BC边所在的直线为x轴建立平面直角坐标系,直线l与y轴重合且向右平移,若其扫过的面积(阴影部分)为S,设向右平移的距离BP为x,则S关于x的函数图象大致是( )| A. | 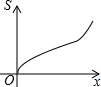 | B. |  | C. | 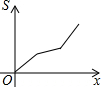 | D. | 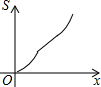 |
分析 根据题意可以分别得到各段对应的函数解析式,从而可以得到相应的函数图象,进而可以得到哪个函数图象是正确的.
解答 解:设∠ABP=α,点A到BC的距离是a,AD的长度是b,
当直线l从y轴重合且向右平移至l过点A的过程中,
S=$\frac{x•tanα•x}{2}=\frac{tanα}{2}{x}^{2}$,
当直线l平移至过点D的过程中,
S=$\frac{a•\frac{a}{tanα}}{2}+a•(x-\frac{a}{tanα})$=$ax-\frac{{a}^{2}}{2tanα}$,
当直线l平移至过点C的过程中,
S=$\frac{(b+b+2×\frac{a}{tanα})•a}{2}-\frac{(b+2×\frac{a}{tanα}-x)•(b+2×\frac{a}{tanα}-x)•tanα}{2}$,
由上可得,刚开始是二次函数图象,然后是一次函数图象,最后是二次函数图象,
故选D.
点评 本题考查动点问题的函数图象,解题的关键是明确题意,可以写出各段的函数解析式,明确各段相应的函数图象.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.下列运算正确的是( )
| A. | a•a2=a2 | B. | (ab)2=ab2 | C. | a6÷a2=a4 | D. | (a2)3=a5 |
18.下列式子中,错误的是( )
| A. | $\sqrt{2}$×$\sqrt{8}$=4 | B. | $\sqrt{(-4)×(-9)}$=$\sqrt{-4}$×$\sqrt{-9}$ | C. | $\sqrt{\frac{4}{3}}$=$\frac{2}{3}$$\sqrt{3}$ | D. | $\frac{4\sqrt{18}}{2\sqrt{6}}$=2$\sqrt{3}$ |
15.若M(-2,y1),N(-1,y2),P(2,y3)三点都在函数y=$\frac{k}{x}$(k<0)的图象上,则y1,y2,y3的大小关系是( )
| A. | y3>y1>y2 | B. | y3>y2>y1 | C. | y1>y2>y3 | D. | y2>y1>y3 |
13.用配方法解方程3x2-$\frac{12}{5}$x-1=0时,变形正确的是( )
| A. | (x+$\frac{2}{5}$)2-$\frac{37}{25}$=0 | B. | 3(x+$\frac{2}{5}$)2-$\frac{37}{25}$=0 | C. | (x-$\frac{2}{5}$)2-$\frac{37}{25}$=0 | D. | 3(x-$\frac{2}{5}$)2-$\frac{37}{25}$=0 |
 如图,菱形ABCD中,两条对角线长AC=8,BD=6,则菱形ABCD的面积为24.
如图,菱形ABCD中,两条对角线长AC=8,BD=6,则菱形ABCD的面积为24.