题目内容
 在四边形ABCD中,∠A=60°,AB⊥BC,AD⊥CD,AB=200米,CD=100米,求AD,BC的长(精确到1米,参考数据
在四边形ABCD中,∠A=60°,AB⊥BC,AD⊥CD,AB=200米,CD=100米,求AD,BC的长(精确到1米,参考数据| 3 |
考点:勾股定理,含30度角的直角三角形
专题:
分析:延长AD交BC的延长线与O,求出∠B=∠ADC=∠CDO=90°,求出∠O=30°,根据含30度角的直角三角形的性质求出OA和OC,根据勾股定理求出OD和OB即可.
解答:解: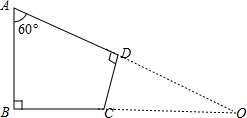
延长AD交BC的延长线与O,
∵AB⊥BC,AD⊥CD,
∴∠B=∠ADC=∠CDO=90°,
∵∠A=60°,
∴∠O=30°,
∵AB=200米,CD=100米,
∴OA=2AB=400米,OC=2CD=200米,
由勾股定理得:OD=
=100
米,OB=
=200
米,
∴AD=OA-OD=(400-100
)米,BC=OB-OC=(200
-200)≈200×(1.732-1)≈146米.

延长AD交BC的延长线与O,
∵AB⊥BC,AD⊥CD,
∴∠B=∠ADC=∠CDO=90°,
∵∠A=60°,
∴∠O=30°,
∵AB=200米,CD=100米,
∴OA=2AB=400米,OC=2CD=200米,
由勾股定理得:OD=
| OC2-CD2 |
| 3 |
| OA2-AB2 |
| 3 |
∴AD=OA-OD=(400-100
| 3 |
| 3 |
点评:本题考查了三角形内角和定理,垂直定义,含30度角的直角三角形的性质,勾股定理的应用,解此题的关键是构造直角三角形,并进一步求出各个边的长,难度适中.

练习册系列答案
相关题目
 如图,△ABC沿边BC所在直线向右平移得到△DEF,则下列结论中错误的是( )
如图,△ABC沿边BC所在直线向右平移得到△DEF,则下列结论中错误的是( )| A、△ABC≌△DEF |
| B、AC=DF |
| C、AB=DE |
| D、EC=FC |
 如图所示,在平行四边形ABCD中,BE、CF平分∠B、∠C,交AD于E、F两点,求证:AF=DE.
如图所示,在平行四边形ABCD中,BE、CF平分∠B、∠C,交AD于E、F两点,求证:AF=DE. 如图,直线CD,EF相交于点O,OA⊥OB,OF平分∠AOD,∠BOE=2∠BOC,求∠BOC的度数.
如图,直线CD,EF相交于点O,OA⊥OB,OF平分∠AOD,∠BOE=2∠BOC,求∠BOC的度数. 如图,在△ABC中,∠B=40°,∠C=110°.按要求完成下列各题.
如图,在△ABC中,∠B=40°,∠C=110°.按要求完成下列各题. 如图,平行四边形ABCD纸片中,AC⊥AB,AC与BD交于点O,沿对角线AC对折后,E与B对应.
如图,平行四边形ABCD纸片中,AC⊥AB,AC与BD交于点O,沿对角线AC对折后,E与B对应. 要用总长为20m的铁栏杆,两面靠墙,围成一个矩形的花圃,怎样围法,才能使围成的花圃面积最大?
要用总长为20m的铁栏杆,两面靠墙,围成一个矩形的花圃,怎样围法,才能使围成的花圃面积最大?