题目内容
某种药品原价为25元/盒,经过连续两次涨价后售价为36元/盒.则平均每次涨价的百分率为 .
考点:一元二次方程的应用
专题:增长率问题
分析:应理解“价格上调”的含义.一般用增长后的量=增长前的量×(1+增长率).设每次调价的百分率是x,则第一次调价后的价格是25(1+x),第二次后的价格是25(1+x)2,据此即可列出方程从而求解.
解答:解:设每次涨价的平均百分率为x,则第一次涨价后的价格为25×(1+x),
那么第二次涨价后的价格用代数式表示为25×(1+x)(1+x),
所以可列方程为:25×(1+x)2=36,
解得:x1=0.2=20%,x2=-2.2,
∵x>0,
∴x=20%.
∴每次涨价的平均百分率为20%.
故答案是:20%.
那么第二次涨价后的价格用代数式表示为25×(1+x)(1+x),
所以可列方程为:25×(1+x)2=36,
解得:x1=0.2=20%,x2=-2.2,
∵x>0,
∴x=20%.
∴每次涨价的平均百分率为20%.
故答案是:20%.
点评:本题主要考查百分率的问题,求平均变化率的方法.若设变化前的量为a,变化后的量为b,平均变化率为x,则经过两次变化后的数量关系为a(1±x)2=b.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
下列说法正确的是( )
A、
| ||
| B、-1<-100 | ||
C、
| ||
| D、-3>0 |
下列因式分解正确的是( )
| A、x3-x=x(x2-1) | ||||
B、y2-y+
| ||||
| C、m2-m+6=(m-2)(m+3) | ||||
| D、a3-4b2=(a+4b)(a-4b) |
 在四边形ABCD中,∠A=60°,AB⊥BC,AD⊥CD,AB=200米,CD=100米,求AD,BC的长(精确到1米,参考数据
在四边形ABCD中,∠A=60°,AB⊥BC,AD⊥CD,AB=200米,CD=100米,求AD,BC的长(精确到1米,参考数据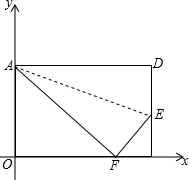 折叠矩形ABCD的一边AD,折痕为AE,且使点D落在BC边上的点F处,已知AB=8cm,BC=10cm,以B点为原点,BC为x轴,BA为y轴建立平面直角坐标系.求点F和点E坐标.
折叠矩形ABCD的一边AD,折痕为AE,且使点D落在BC边上的点F处,已知AB=8cm,BC=10cm,以B点为原点,BC为x轴,BA为y轴建立平面直角坐标系.求点F和点E坐标.