题目内容
 如图,平行四边形ABCD纸片中,AC⊥AB,AC与BD交于点O,沿对角线AC对折后,E与B对应.
如图,平行四边形ABCD纸片中,AC⊥AB,AC与BD交于点O,沿对角线AC对折后,E与B对应.(1)试问:四边形ACDE是什么形状的四边形?请加以证明;
(2)若其他条件不变还应具备一个什么条件时,EO平分∠AOD成立?说明其理由;
(3)若四边形ABCD的面积S=12cm,设CE、AD交于点F,求翻转后纸片重叠部分的面积,即S△ACF.
考点:翻折变换(折叠问题),平行四边形的性质,矩形的判定与性质
专题:
分析:(1)首先证明AE∥CD,AE=CD,得到四边形ACDE为平行四边形;证明∠EAC=90°,即可解决问题.
(2)若OE平分∠AOD,则∠AOE=∠DOE;而∠AOB=∠AOE,故必有∠AOB=∠AOE=∠EOD=60°.
(3)运用矩形(或平行四边形)将矩形分割为面积相等的四部分,即可解决问题.
(2)若OE平分∠AOD,则∠AOE=∠DOE;而∠AOB=∠AOE,故必有∠AOB=∠AOE=∠EOD=60°.
(3)运用矩形(或平行四边形)将矩形分割为面积相等的四部分,即可解决问题.
解答: 解:(1)四边形ACDE是矩形;理由如下:
解:(1)四边形ACDE是矩形;理由如下:
∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD;而AB⊥AC,
∴∠BAC=∠DCA=90°;由题意得:
AE=AB,∠EAO=∠BAO=90°,
∴AE∥CD,AE=CD,且∠EAC=90°,
∴四边形ACDE是矩形.
(2)当∠AOB=60°时,EO平分∠AOD;理由如下:
由题意得:∠AOE=∠AOB=60°,
∴∠DOE=180°-120°=60°,
∴∠AOE=∠DOE,即EO平分∠AOD.
(3)∵平行四边形ABCD的面积S=12,
∴S△ACD=
SABCD=6;同理可知:
S△ACF=
S△ACD=3.
 解:(1)四边形ACDE是矩形;理由如下:
解:(1)四边形ACDE是矩形;理由如下:∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD;而AB⊥AC,
∴∠BAC=∠DCA=90°;由题意得:
AE=AB,∠EAO=∠BAO=90°,
∴AE∥CD,AE=CD,且∠EAC=90°,
∴四边形ACDE是矩形.
(2)当∠AOB=60°时,EO平分∠AOD;理由如下:
由题意得:∠AOE=∠AOB=60°,
∴∠DOE=180°-120°=60°,
∴∠AOE=∠DOE,即EO平分∠AOD.
(3)∵平行四边形ABCD的面积S=12,
∴S△ACD=
| 1 |
| 2 |
S△ACF=
| 1 |
| 2 |
点评:该题主要考查了平行四边形的性质、翻折变换的性质、矩形的判定与性质等几何知识点及其应用问题;解题的关键是牢固掌握平行四边形的性质、翻折变换的性质等知识点.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 在四边形ABCD中,∠A=60°,AB⊥BC,AD⊥CD,AB=200米,CD=100米,求AD,BC的长(精确到1米,参考数据
在四边形ABCD中,∠A=60°,AB⊥BC,AD⊥CD,AB=200米,CD=100米,求AD,BC的长(精确到1米,参考数据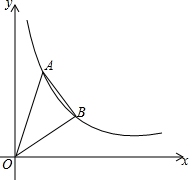 如图,在平面直角坐标系中,直线y=4x、y=x分别与双曲线y=
如图,在平面直角坐标系中,直线y=4x、y=x分别与双曲线y=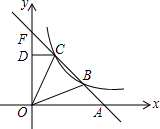 如图,直线y=-2x+8与x轴交于A点,与双曲线y=
如图,直线y=-2x+8与x轴交于A点,与双曲线y= 函数y=x2+bx+c与y=x的图象如图所示,下面结论:①b2-4c>0,②b+c+1=0,③3b+c+6=0,④当1<x<3时,x2+(b-1)x+c<0,其中正确的是( )
函数y=x2+bx+c与y=x的图象如图所示,下面结论:①b2-4c>0,②b+c+1=0,③3b+c+6=0,④当1<x<3时,x2+(b-1)x+c<0,其中正确的是( )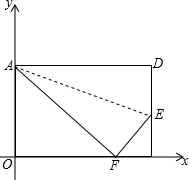 折叠矩形ABCD的一边AD,折痕为AE,且使点D落在BC边上的点F处,已知AB=8cm,BC=10cm,以B点为原点,BC为x轴,BA为y轴建立平面直角坐标系.求点F和点E坐标.
折叠矩形ABCD的一边AD,折痕为AE,且使点D落在BC边上的点F处,已知AB=8cm,BC=10cm,以B点为原点,BC为x轴,BA为y轴建立平面直角坐标系.求点F和点E坐标. 如图,∠AOB=90°,直线CD将∠AOB分成2:3两部分,∠AOC大于∠BOC,那么∠BOC=
如图,∠AOB=90°,直线CD将∠AOB分成2:3两部分,∠AOC大于∠BOC,那么∠BOC=