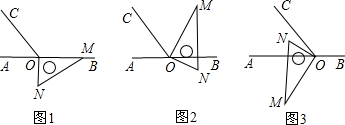
题目内容
已知直角三角形ABC中,∠B=90°,AB=8,BC=6,BM为中线,△BMN为等腰三角形(点N在三角形AB或AC边上,且不与顶点重合),求S△BMN.
考点:三角形中位线定理,直角三角形斜边上的中线,勾股定理
专题:分类讨论
分析:根据勾股定理求得AC的长,然后根据直角三角形斜边上的中线等于斜边的一半确定N一定在AB上,作MG⊥AB,则MG是△ABC的中位线,然后利用三角形的面积公式求解.
解答:解: 在直角△ABC中,AC=
在直角△ABC中,AC=
=
=10,
∵BM为中线,
∴BM=CM=AM=
AC=5.
则N一定在AB上,且BM=BN=5,作MG⊥AB于点G.
∵M是AC的中点,且MG∥BC,
∴MG是△ABC的中位线,
∴MG=
BC=
×6=3,
∴S△BMN=
BN•MG=
×5×3=
.
 在直角△ABC中,AC=
在直角△ABC中,AC=| AB2+BC2 |
| 82+62 |
∵BM为中线,
∴BM=CM=AM=
| 1 |
| 2 |
则N一定在AB上,且BM=BN=5,作MG⊥AB于点G.
∵M是AC的中点,且MG∥BC,
∴MG是△ABC的中位线,
∴MG=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△BMN=
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 2 |
点评:本题考查了直角三角形的性质以及三角形的中位线定理,确定N在AB边上是关键.

练习册系列答案
相关题目
下列因式分解正确的是( )
| A、x3-x=x(x2-1) | ||||
B、y2-y+
| ||||
| C、m2-m+6=(m-2)(m+3) | ||||
| D、a3-4b2=(a+4b)(a-4b) |
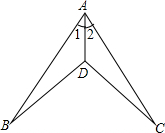 如图,已知∠1=∠2,∠B=∠C,若直接推得△ABD≌△ACD,则其根据是( )
如图,已知∠1=∠2,∠B=∠C,若直接推得△ABD≌△ACD,则其根据是( )| A、SAS | B、SSS |
| C、ASA | D、AAS |
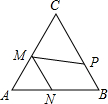 如图,在等边△ABC中,AB=4,P、M、N分别是BC,CA、AB边上动点,则PM+MN的最小值是
如图,在等边△ABC中,AB=4,P、M、N分别是BC,CA、AB边上动点,则PM+MN的最小值是 在四边形ABCD中,∠A=60°,AB⊥BC,AD⊥CD,AB=200米,CD=100米,求AD,BC的长(精确到1米,参考数据
在四边形ABCD中,∠A=60°,AB⊥BC,AD⊥CD,AB=200米,CD=100米,求AD,BC的长(精确到1米,参考数据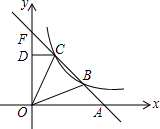 如图,直线y=-2x+8与x轴交于A点,与双曲线y=
如图,直线y=-2x+8与x轴交于A点,与双曲线y=