题目内容
 如图,在△ABC中,∠B=40°,∠C=110°.按要求完成下列各题.
如图,在△ABC中,∠B=40°,∠C=110°.按要求完成下列各题.(1)画出△ABC的高AD;
(2)画出△ABC的角平分线AE;
(3)根据你所画的图形求∠DAE的度数.
考点:作图—复杂作图
专题:
分析:(1)过A点作AD⊥BC于D,AD就是所求的高;
(2)以点A为圆心,以任意长为半径画弧,交AB,AC于两点,分别以这两点为圆心,大于这两点的距离的一半为半径画弧,在∠CAB的内部交于一点,过这一点及点A作直线交BC于点E,AE就是所求的∠A的平分线;
(3)利用角平分线把一个角平分的性质和高线的性质可得∠DAE的度数.
(2)以点A为圆心,以任意长为半径画弧,交AB,AC于两点,分别以这两点为圆心,大于这两点的距离的一半为半径画弧,在∠CAB的内部交于一点,过这一点及点A作直线交BC于点E,AE就是所求的∠A的平分线;
(3)利用角平分线把一个角平分的性质和高线的性质可得∠DAE的度数.
解答: 解:(1)如图,AD即为所求作的高;
解:(1)如图,AD即为所求作的高;
(2)如图,AE即为所求作的角平分线;
(3)在△ABC中,∵∠B=40°,∠C=110°,
∴∠CAB=180°-40°-110°=30°,
∵AE平分∠CAB,
∴∠EAB=
∠CAB=15°,
∵∠AED是△ABE的外角,
∴∠AED=∠B+∠EAB=55°,
∵AD⊥BC,
∴∠ADB=90°,
∴在Rt△ADE中,
∠DAE=90°-∠AED=90°-55°=35°.
 解:(1)如图,AD即为所求作的高;
解:(1)如图,AD即为所求作的高; (2)如图,AE即为所求作的角平分线;
(3)在△ABC中,∵∠B=40°,∠C=110°,
∴∠CAB=180°-40°-110°=30°,
∵AE平分∠CAB,
∴∠EAB=
| 1 |
| 2 |
∵∠AED是△ABE的外角,
∴∠AED=∠B+∠EAB=55°,
∵AD⊥BC,
∴∠ADB=90°,
∴在Rt△ADE中,
∠DAE=90°-∠AED=90°-55°=35°.
点评:考查三角形的高与角平分线的画法;求三角形同一顶点处的高线与角平分线的夹角注意运用角平分线的性质,高线的性质,以及三角形内角和定理.

练习册系列答案
相关题目

 在四边形ABCD中,∠A=60°,AB⊥BC,AD⊥CD,AB=200米,CD=100米,求AD,BC的长(精确到1米,参考数据
在四边形ABCD中,∠A=60°,AB⊥BC,AD⊥CD,AB=200米,CD=100米,求AD,BC的长(精确到1米,参考数据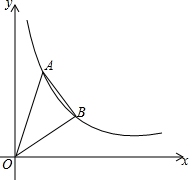 如图,在平面直角坐标系中,直线y=4x、y=x分别与双曲线y=
如图,在平面直角坐标系中,直线y=4x、y=x分别与双曲线y= 函数y=x2+bx+c与y=x的图象如图所示,下面结论:①b2-4c>0,②b+c+1=0,③3b+c+6=0,④当1<x<3时,x2+(b-1)x+c<0,其中正确的是( )
函数y=x2+bx+c与y=x的图象如图所示,下面结论:①b2-4c>0,②b+c+1=0,③3b+c+6=0,④当1<x<3时,x2+(b-1)x+c<0,其中正确的是( ) 如图,在3×3的方格纸中,每个小方格都是边长为1的正方形,O,A,B是格点,求
如图,在3×3的方格纸中,每个小方格都是边长为1的正方形,O,A,B是格点,求